Bài 8.40 trang 89 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đường thẳng và mặt phẳng trong không gian. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về vectơ, phương trình đường thẳng và mặt phẳng.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự. Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong SGK Toán 11.
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a.
Đề bài
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Góc tạo bởi cạnh bên và mặt đáy bằng 600. Hình chiếu của A trên mặt phẳng (A’B’C’) là trung điểm H của cạnh B’C’.
a ) Tính khoảng cách giữa hai mặt đáy của hình lăng trụ này.
b) Tính số đo của góc nhị diện tạo bởi mặt bên (ABB’A’) và mặt đáy (A’B’C’).
Phương pháp giải - Xem chi tiết
Tìm a, b lần lượt vuông góc với (P) và (Q) thì góc giữa a và b là góc giữa (P) và (Q).
Lời giải chi tiết
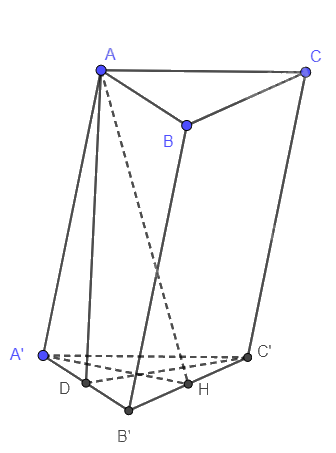
a) Góc giữa AA’ và (A’B’C’) là góc AA’H. Suy ra \(\widehat {AA'H} = {60^0}\)
Tam giác A’B’C’ đều cạnh a nên A’H = \(\frac{{\sqrt 3 }}{2}a\)
\(AH = A'H.\tan {60^0} = \frac{{\sqrt 3 }}{2}a.\sqrt 3 = \frac{3}{2}a\)
b) Gọi D là trung điểm A’B’
Góc giữa (ABB’A’) và (A’B’C’) là góc ADC’.
Bài 8.40 trang 89 SGK Toán 11 tập 2 yêu cầu giải một bài toán về vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Phân tích bài toán:
Trước khi bắt tay vào giải, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho (phương trình đường thẳng, phương trình mặt phẳng) và yêu cầu của bài toán (xác định vị trí tương đối, tìm giao điểm, tính khoảng cách,...). Sau đó, chúng ta sẽ áp dụng các kiến thức đã học để giải quyết bài toán.
Lời giải chi tiết:
(Ở đây sẽ là lời giải chi tiết của bài toán Bài 8.40 trang 89 SGK Toán 11 tập 2. Lời giải sẽ bao gồm các bước sau:)
Ví dụ minh họa:
(Ở đây sẽ có một ví dụ minh họa cụ thể về cách giải bài toán tương tự, giúp học sinh hiểu rõ hơn về phương pháp giải.)
Lưu ý quan trọng:
Bài tập tương tự:
(Ở đây sẽ có một số bài tập tương tự để học sinh luyện tập và củng cố kiến thức.)
Tổng kết:
Bài 8.40 trang 89 SGK Toán 11 tập 2 là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải các bài toán về vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Việc nắm vững các kiến thức và phương pháp giải bài toán này sẽ giúp học sinh tự tin hơn khi làm bài kiểm tra và thi cử.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những lưu ý quan trọng trên, các em học sinh sẽ hiểu rõ hơn về bài toán này và đạt kết quả tốt trong học tập.