Chào mừng các em học sinh đến với lời giải chi tiết Bài 8.23 trang 79 SGK Toán 11 tập 2. Bài học này thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải bài tập Toán 11 một cách rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt đáy (ABCD). Tỉnh khoảng cách từ B đến (SCD).
Phương pháp giải - Xem chi tiết
Tìm khoảng cách giữa M và (P):
+ Tìm (Q) chứa M và vuông góc với (P) theo giao tuyến d.
+ Từ M hạ MH vuông góc với d (H thuộc d).
+ Khi đó MH là khoảng cách cần tìm.
Lời giải chi tiết
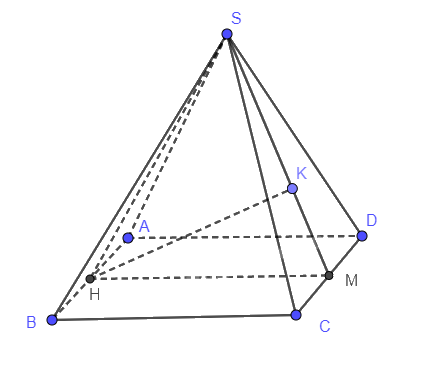
Gọi H, M lần lượt là trung điểm của AB, CD. Kẻ HK vuông góc với SM
Vì AB // CD nên AB // (SCD)
Do đó \(d\left( {B'\left( {SCD} \right)} \right) = d\left( {H;\left( {SCD} \right)} \right) = HK\)
\(\begin{array}{l}\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{M^2}}}\\ \Rightarrow HK = \frac{{\sqrt {21} }}{7}\end{array}\)
Bài 8.23 trang 79 SGK Toán 11 tập 2 yêu cầu chúng ta giải quyết một bài toán liên quan đến việc tìm cực trị của hàm số. Để giải bài toán này, chúng ta cần nắm vững các bước sau:
Giải bài toán cụ thể:
Giả sử bài toán yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Bước 1: Tập xác định: Hàm số f(x) xác định trên R.
Bước 2: Đạo hàm bậc nhất: f'(x) = 3x2 - 6x.
Bước 3: Điểm dừng: Giải phương trình 3x2 - 6x = 0, ta được x = 0 hoặc x = 2.
Bước 4: Khảo sát dấu của đạo hàm:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | + |
| f(x) | ↗ | ↘ | ↗ | ↗ |
Bước 5: Kết luận:
Lưu ý quan trọng:
Trong quá trình giải bài toán, cần chú ý kiểm tra lại các bước tính toán để đảm bảo tính chính xác. Ngoài ra, việc vẽ đồ thị hàm số có thể giúp chúng ta hình dung rõ hơn về sự biến thiên của hàm số và xác định các điểm cực trị một cách trực quan.
Mở rộng kiến thức:
Để hiểu sâu hơn về cực trị của hàm số, các em có thể tìm hiểu thêm về các khái niệm liên quan như điểm uốn, tiệm cận và ứng dụng của đạo hàm trong việc giải quyết các bài toán tối ưu hóa.
Bài tập tương tự:
Các em có thể luyện tập thêm với các bài tập tương tự trong SGK Toán 11 tập 2 hoặc các đề thi thử để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Tổng kết:
Bài 8.23 trang 79 SGK Toán 11 tập 2 là một bài toán quan trọng giúp các em hiểu rõ hơn về ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Hy vọng với lời giải chi tiết và các lưu ý quan trọng trên, các em sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.