Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 46, 47 SGK Toán 11 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 11.
Bài học này tập trung vào các kiến thức quan trọng về... (Nội dung cụ thể về kiến thức trọng tâm của mục 2 sẽ được điền vào đây sau khi xác định nội dung chính xác)
Một vật chuyển động thẳng với phương trình \(s\left( t \right) = {t^3} + t\), với \(s\) tính bằng mét và \(t\) tính bằng giây
Một vật chuyển động thẳng với phương trình \(s\left( t \right) = {t^3} + t\), với \(s\) tính bằng mét và \(t\) tính bằng giây
a) Tính vận tốc của vật tại thời điểm \(t\).
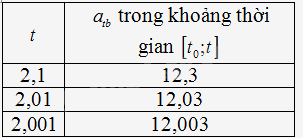
b) Cho biết gia tốc trung bình (đơn vị \(m/{s^2}\)) của vật trong khoảng thời gian \(\left[ {{t_0};t} \right]\) được tính bởi công thức \({a_{tb}} = \frac{{v\left( t \right) - v\left( {{t_0}} \right)}}{{t - {t_0}}}\). Hãy tính gia tốc trung bình trong các khoảng thời gian \(\left[ {{t_0};t} \right]\) với \({t_0} = 2\) và \(t\) lần lượt là \(2,1\); \(2,01\); \(2,001\). Sau đó, hoàn thành Bảng 7.3.

Phương pháp giải:
a) \(v\left( t \right) = s'\left( t \right)\); công thức tính đạo hàm \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\)
b) Tính \({a_{tb}} = \frac{{v\left( t \right) - v\left( {{t_0}} \right)}}{{t - {t_0}}}\). Sau đó thay \(t\) và \({t_0}\) vào \({a_{tb}}\)
Lời giải chi tiết:
a) Vận tốc của vật tại thời điểm \(t\) là \(v\left( t \right) = s'\left( t \right) = \left( {{t^3} + t} \right)' = 3{t^2} + 1\)
b) \(v\left( t \right) - v\left( {{t_0}} \right) = \left( {3{t^2} + 1} \right) - \left( {3t_0^2 + 1} \right) = 3\left( {t - {t_0}} \right)\left( {t + {t_0}} \right)\)
Suy ra \({a_{tb}} = \frac{{v\left( t \right) - v\left( {{t_0}} \right)}}{{t - {t_0}}} = 3\left( {t + {t_0}} \right)\) tại \({t_0} = 2\) là \({a_{tb}} = 3\left( {t + 2} \right)\)
+) Với \(t = 2,1\) ta có \({a_{tb}} = 3.\left( {2,1 + 2} \right) = 12,3\)
+) Với \(t = 2,01\) ta có \({a_{tb}} = 3.\left( {2,01 + 2} \right) = 12,03\)
+) Với \(t = 2,001\) ta có \({a_{tb}} = 3.\left( {2,001 + 2} \right) = 12,003\)
Vậy ta có bảng sau
Phương trình chuyển động của một con lắc lò xo dao động quanh vị trí cân bằng \(O\) là \(x = 4\cos 2t\), trong đó \(t\) tính bằng giây và \(x\) tính bằng \(cm\). Tính gia tốc của con lắc tại thời điểm \(t\).
Phương pháp giải:
+) \(a\left( t \right) = x''\left( t \right)\)
+) \(\left( {\cos u} \right) = - u'.\sin u;\,\,\,\left( {\sin u} \right) = u'.\cos u\)
Lời giải chi tiết:
Ta có \(x' = \left( {4\cos 2t} \right)' = - 4.\sin 2t.\left( {2t} \right)' = - 8\sin 2t\)
\(a\left( t \right) = x'' = - 8.\cos 2t.\left( {2t} \right)' = - 16\cos 2t\)
Mục 2 của SGK Toán 11 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Bài tập trong mục 2 trang 46, 47 SGK Toán 11 tập 2 thường yêu cầu học sinh:
Để giải bài tập này, ta áp dụng quy tắc tính đạo hàm của tổng và hiệu, cũng như quy tắc tính đạo hàm của lũy thừa:
f'(x) = 3x^2 - 4x + 5
Ở bài này, ta cần sử dụng quy tắc tính đạo hàm của hàm hợp và đạo hàm của các hàm lượng giác:
g'(x) = 2cos(2x) - sin(x)
Đầu tiên, ta tính đạo hàm cấp một:
h'(x) = 4x^3 - 6x
Sau đó, ta tính đạo hàm cấp hai:
h''(x) = 12x^2 - 6
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Khi giải bài tập đạo hàm, cần lưu ý một số điểm sau:
Việc giải bài tập mục 2 trang 46, 47 SGK Toán 11 tập 2 đòi hỏi sự nắm vững kiến thức về đạo hàm và khả năng áp dụng các quy tắc tính đạo hàm một cách linh hoạt. Hy vọng với hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em học sinh sẽ tự tin giải các bài tập và đạt kết quả tốt trong môn Toán.