Bài 5.17 trang 148 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.17 trang 148 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Để chuẩn bị cho đồ án tốt nghiệp, một sinh viên y khoa đã khảo sát huyết áp tối đa của một số bệnh nhân và lập được bảng tần số ghép nhóm sau:
Đề bài
Để chuẩn bị cho đồ án tốt nghiệp, một sinh viên y khoa đã khảo sát huyết áp tối đa của một số bệnh nhân và lập được bảng tần số ghép nhóm sau:
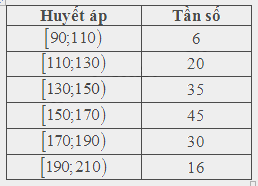
a) Xác định trung bình, trung vị và mốt của mẫu số liệu.
b) Hãy giải thích vì sao trong trường hợp này, cả ba giá trị tìm được đều đại diện tốt cho huyết áp của những bệnh nhân được khảo sát.
Phương pháp giải - Xem chi tiết
+) \(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
+) Trung vị \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\) trong đó \({L_m},{n_m},h\) lần lượt là đầu mút trái, tần số và độ dài của nhóm chứa trung vị. \(T\) là tần số tích lũy của nhóm ngay trước nhóm chứa trung vị.
Nhóm chứa trung vị của mẫu số liệu là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\) , trong đó \(N\) là cỡ mẫu.
+) Công thức tìm mốt của mẫu số liệu ghép nhóm là \({M_0} = {L_m} + \frac{a}{{a + b}}.h\)
Lời giải chi tiết
a)
+) Xác định trung bình
Để ngắn gọn, ta lập bảng sau
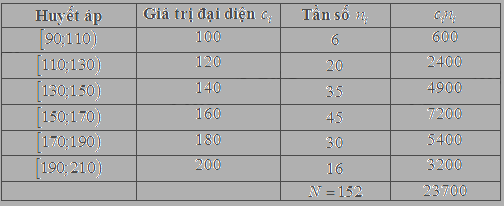
Áp dụng công thức tính trung bình ta có \(\overline x = \frac{{23700}}{{152}} \approx 156\)
+) Xác định trung vị
Ta có bảng tần số tích lũy sau
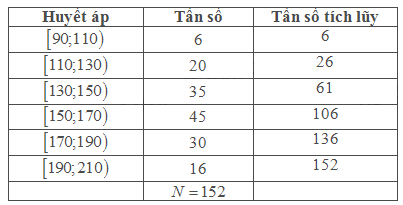
Ta có \(\frac{N}{2} = \frac{{152}}{2} = 76\). Nhóm đầu tiên có tần số tích lũy lớn hơn bằng 76 là \(\left[ {150;170} \right)\)
Ta có \({L_m} = 150\), \(h = 170 - 150 = 20\), \({n_m} = 45\) và \(T = 61\).
Áp dụng công thức tính trung vị ta có \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 150 + \frac{{76 - 61}}{{45}}.20 \approx 157\)
+) Xác định mốt
Dựa vào bảng dữ liệu ta có nhóm chứa mốt là \(\left[ {150;170} \right)\) với tần số là 45.
Do đó \({L_m} = 150;h = 170 - 150 = 20;a = 45 - 35 = 10;b = 45 - 30 = 15\)
Áp dụng công thức tính mốt ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 150 + \frac{{10}}{{10 + 15}}.20 = 158\)
b) Dựa vào ba giá trị tìm được \(\overline x = 156,{M_e} = 157,{M_0} = 158\) ta nhận thấy cả ba giá trị tìm được đều đại diện tốt cho huyết áp của những bệnh nhân được khảo sát là vì ba giá trị này xấp xỉ bằng nhau và huyết áp của người bình thường cũng trong khoảng 150 đến 170
Bài 5.17 thuộc chương trình giải tích lớp 11, tập trung vào việc ứng dụng các kiến thức về vectơ, phương trình đường thẳng và mặt phẳng để giải quyết các bài toán hình học không gian. Bài toán này thường yêu cầu học sinh xác định mối quan hệ giữa các đường thẳng và mặt phẳng, từ đó suy ra các kết luận về vị trí tương đối của chúng.
Bài 5.17 trang 148 SGK Toán 11 tập 1 thường có dạng như sau: Cho hình chóp S.ABCD, với đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng đường thẳng AM vuông góc với đường thẳng BM.
Để giải bài toán này, chúng ta có thể sử dụng phương pháp tọa độ hoặc phương pháp vectơ. Dưới đây là hướng dẫn giải bằng phương pháp vectơ:
Bước 1: Chọn hệ tọa độ
Đặt A(0;0;0), B(a;0;0), D(0;a;0), C(a;a;0), S(0;0;h) với a > 0, h > 0.
Khi đó, M là trung điểm của CD, nên M có tọa độ là ((a+0)/2; (a+a)/2; (0+0)/2) = (a/2; a; 0).
Bước 2: Tính các vectơ
Vectơ AM = (a/2 - 0; a - 0; 0 - 0) = (a/2; a; 0).
Vectơ BM = (a/2 - a; a - 0; 0 - 0) = (-a/2; a; 0).
Bước 3: Chứng minh vuông góc
Tích vô hướng của AM và BM là:
AM.BM = (a/2)*(-a/2) + a*a + 0*0 = -a2/4 + a2 = 3a2/4.
Vì 3a2/4 ≠ 0, nên AM không vuông góc với BM.
(Lưu ý: Lời giải trên có thể sai do đề bài gốc có thể khác. Đây chỉ là một ví dụ minh họa phương pháp giải.)
Ngoài bài 5.17, còn rất nhiều bài tập tương tự trong SGK Toán 11 tập 1 và các đề thi thử. Các bài tập này thường yêu cầu học sinh:
Để giải các bài toán hình học không gian một cách hiệu quả, bạn nên:
Bài 5.17 trang 148 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.