Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 95 và 96 sách giáo khoa Toán 11 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Đây là ảnh chụp một góc bên trong căn phòng. Xem các mép tường (cạnh tường) là hình ảnh của đường thẳng.
Đây là ảnh chụp một góc bên trong căn phòng. Xem các mép tường (cạnh tường) là hình ảnh của đường thẳng. Hãy chỉ ra một số cặp đường thẳng cùng nằm trong mặt phẳng và một số cặp đường thẳng không thể cùng nằm trong một mặt phẳng.
Phương pháp giải:
Quan sát hình ảnh.
Lời giải chi tiết:
Mép tường bên trái, bên phải, bên trên, bên dưới của một bức tường nằm trong cùng một mặt phẳng.
Mép tường bên trái của bức tường chính giữa và mép tường bên trên/dưới của bức tường bên phải không cùng nằm trong một mặt phẳng.
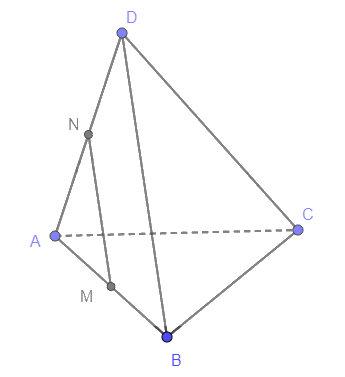
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và AD. Chứng minh đường thẳng MN song song với đường thẳng BD và đường thẳng AB chéo với đường thẳng CD. Hãy chỉ ra thêm một cặp đường thẳng chéo nhau khác của tứ diện này.
Phương pháp giải:
Hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.
Hai đường thẳng chéo nhau là hai đường thẳng không đồng phẳng.
Lời giải chi tiết:

Ta có: MN và BD song song do cùng nằm trong mặt phẳng (ABD) và không có điểm chung (Đường trung bình của tam giác).
Giả sử AB và CD cùng nằm trong một mặt phẳng. Suy ra A, B, C, D cùng nằm trong một mặt phẳng. Điều này mâu thuẫn với giả thiết. Vậy AB và CD chéo nhau.
Giả sử AD và BC cùng nằm trong một mặt phẳng. Suy ra A, B, C, D cùng nằm trong một mặt phẳng. Điều này mâu thuẫn với giả thiết. Vậy AD và BC chéo nhau.
Mục 1 của chương trình Toán 11 tập 1 thường tập trung vào các kiến thức cơ bản về dãy số, cấp số cộng, cấp số nhân. Việc nắm vững các khái niệm, công thức và phương pháp giải bài tập trong mục này là nền tảng quan trọng để học tốt các kiến thức tiếp theo.
Bài tập về dãy số thường yêu cầu học sinh xác định số hạng tổng quát của dãy, tính tổng các số hạng của dãy, hoặc chứng minh một số tính chất của dãy. Để giải các bài tập này, cần nắm vững định nghĩa dãy số, các loại dãy số (dãy số hữu hạn, dãy số vô hạn, dãy số tăng, dãy số giảm) và các công thức tính tổng của dãy số.
Cấp số cộng là một dãy số đặc biệt, trong đó hiệu giữa hai số hạng liên tiếp là một hằng số. Các bài tập về cấp số cộng thường yêu cầu học sinh tìm số hạng tổng quát, tính tổng các số hạng, hoặc chứng minh một số tính chất của cấp số cộng. Công thức quan trọng cần nhớ là un = u1 + (n-1)d và Sn = n(u1 + un)/2.
Ví dụ 2: Tìm số hạng thứ 5 và tổng của 5 số hạng đầu tiên của cấp số cộng có u1 = 3 và d = 2.
Lời giải: u5 = u1 + (5-1)d = 3 + 4(2) = 11. S5 = 5(u1 + u5)/2 = 5(3 + 11)/2 = 35.
Cấp số nhân là một dãy số đặc biệt, trong đó thương giữa hai số hạng liên tiếp là một hằng số. Các bài tập về cấp số nhân tương tự như cấp số cộng, nhưng sử dụng công thức khác. Công thức quan trọng cần nhớ là un = u1 * qn-1 và Sn = u1(1 - qn)/(1 - q) (với q ≠ 1).
Ví dụ 3: Tìm số hạng thứ 4 và tổng của 4 số hạng đầu tiên của cấp số nhân có u1 = 1 và q = 2.
Lời giải: u4 = u1 * q3 = 1 * 23 = 8. S4 = 1(1 - 24)/(1 - 2) = 15.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em nên làm thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu khác. Ngoài ra, các em có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kinh nghiệm và học hỏi lẫn nhau.
Hy vọng với bài viết này, các em đã nắm vững kiến thức và phương pháp giải các bài tập trong mục 1 trang 95, 96 SGK Toán 11 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!