Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 17, 18, 19 của sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Một thí nghiệm cho thấy trong điều kiện môi trường sống lí tưởng
Một thí nghiệm cho thấy trong điều kiện môi trường sống lí tưởng và thức ăn dồi dào thì số lượng của một đàn chuột sẽ gấp đôi sau 55 ngày (nguồn: https://baotintuc.vn/ho-so/ky-la-thi-nghiem-xay-dung-xa-hoi-khong-tuong-cho-chuot-20181226104302132.htm).
Giả sử lúc đầu, đàn chuột có 100 con. Như vậy, sau thời gian t ngày, số lượng chuột là \(P = {100.2^{\frac{t}{{55}}}}\) con.
a) Mất bao lâu để đàn chuột đạt số lượng 2 000 con?
b) Tìm một hàm số t theo P để xác định thời gian t mà số lượng chuột đạt tới P (nếu có).
Phương pháp giải:
Thay P = 2000 vào \(P = {100.2^{\frac{t}{{55}}}}\). Tìm t.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}{100.2^{\frac{t}{{55}}}} = 2000\\ \Leftrightarrow {2^{\frac{t}{{55}}}} = 20\\ \Leftrightarrow \frac{t}{{55}} = {\log _2}20\\ \Leftrightarrow t = 55.{\log _2}20\\ \Leftrightarrow t \approx 237,71\end{array}\)
b)
\(\begin{array}{l}P = {100.2^{\frac{t}{{55}}}}\\ \Leftrightarrow \frac{P}{{100}} = {2^{\frac{t}{{55}}}}\\ \Leftrightarrow \frac{t}{{55}} = {\log _2}\frac{P}{{100}}\\ \Leftrightarrow t = 55.{\log _2}\frac{P}{{100}}\end{array}\)
Vậy hàm số t theo P để xác định thời gian t mà số lượng chuột đạt tới P là: \(t = 55.{\log _2}\frac{P}{{100}}\)
Tìm tập xác định của hàm số sau:
a) \(y = \log \left( {2x - 3} \right)\)
b) \(y = 2 + {\log _{0,5}}\left( {{x^2} - 1} \right)\)
c) \(y = \ln \frac{{3x + 2}}{{1 - x}}\)
Phương pháp giải:
Hàm số \(y = {\log _a}\left( {u\left( x \right)} \right)\left( {a > 0,a \ne 1} \right)\) xác định khi \(u\left( x \right) > 0\).
Lời giải chi tiết:
a) \(y = \log \left( {2x - 3} \right)\) xác định khi \(2x - 3 > 0 \Leftrightarrow x > \frac{3}{2}\)
Vậy \(D = \left( {\frac{3}{2}; + \infty } \right)\)
b) \(y = 2 + {\log _{0,5}}\left( {{x^2} - 1} \right)\) xác định khi \({x^2} - 1 > 0 \Leftrightarrow {x^2} > 1 \Leftrightarrow \left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\)
Vậy \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
c) \(y = \ln \frac{{3x + 2}}{{1 - x}}\) xác định khi \(\frac{{3x + 2}}{{1 - x}} > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}3x + 2 > 0\\1 - x > 0\end{array} \right.\\\left\{ \begin{array}{l}3x + 2 < 0\\1 - x < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > - \frac{2}{3}\\x < 1\end{array} \right.\\\left\{ \begin{array}{l}x < - \frac{2}{3}\\x > 1\end{array} \right.\,{\rm{(L)}}\end{array} \right.\)
Vậy \(D = \left( {\frac{{ - 2}}{3};1} \right)\)
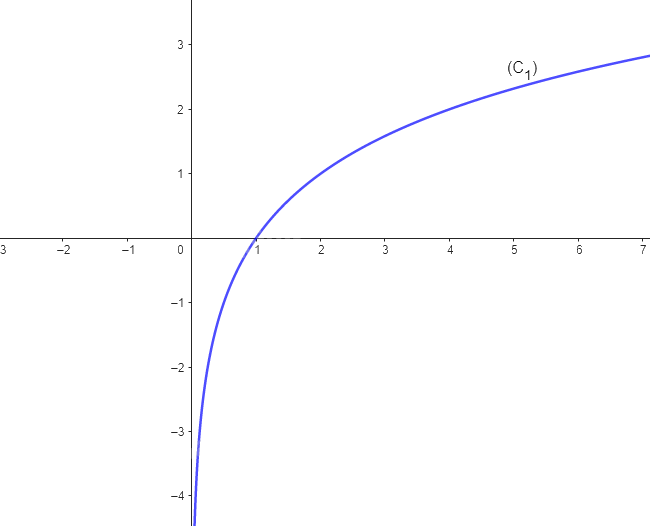
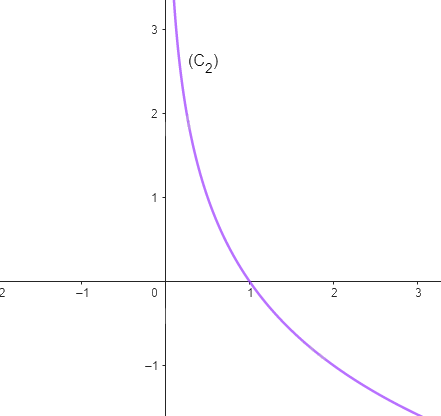
Cho hàm số \(y = {\log _2}x\) có đồ thị là (C1) và hàm số \(y = {\log _{0,5}}x\) có đồ thị (C2).
a) Hoàn thành bảng giá trị sau và biểu diễn trên hệ trục Oxy.
b) Vẽ đường cong nối các điểm thuộc (C1) (theo thứ tự hoành độ tăng dần) và một đường cong khác nối các điểm thuộc (C2) (theo thứ tự hoành độ tăng dần).
Phương pháp giải:
Thay lần lượt các giá trị của x vào hàm số.
Lời giải chi tiết:
a,

b,
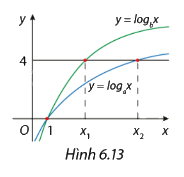
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như Hình 6.13. Đường thẳng y = 4 cắt hai đồ thị tại các điểm có hoành độ x1, x2. Biết rằng x1 = 2x2. Tính giá trị của \(\frac{a}{b}\).

Phương pháp giải:
Thay y = 4 vào 2 hàm số. Áp dụng: \({\log _a}b = c \Leftrightarrow {a^c} = b\) để tính a, b lần lượt theo \({x_1},{x_2}\).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}{\log _a}{x_1} = 4\\ \Leftrightarrow {a^4} = {x_1}\\ \Leftrightarrow {a^4} = 2{x_2}\\ \Leftrightarrow a = {\left( {2{x_2}} \right)^{\frac{1}{4}}}\end{array}\)
\(\begin{array}{l}{\log _b}{x_2} = 4\\ \Leftrightarrow {b^4} = {x_2}\\ \Leftrightarrow b = {\left( {{x_2}} \right)^{\frac{1}{4}}}\end{array}\)
\( \Rightarrow \frac{a}{b} = \frac{{{{\left( {2{x_2}} \right)}^{\frac{1}{4}}}}}{{{{\left( {{x_2}} \right)}^{\frac{1}{4}}}}} = {2^{\frac{1}{4}}}\)
Mục 2 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu rõ bản chất của vấn đề.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến giới hạn). Để giải bài tập này, ta cần...
Bài tập này liên quan đến... (giả sử bài tập liên quan đến đạo hàm). Để giải quyết bài toán này, chúng ta sẽ sử dụng phương pháp...
Bài tập này đòi hỏi học sinh phải kết hợp kiến thức về... (giả sử bài tập liên quan đến ứng dụng đạo hàm). Lời giải chi tiết như sau:
...
Khi giải các bài tập Toán 11 tập 2, các em cần lưu ý những điều sau:
Để giúp các em hiểu rõ hơn, chúng ta sẽ xem xét một ví dụ minh họa:
Ví dụ: Giải phương trình...
Lời giải:...
Hy vọng rằng, với những lời giải chi tiết và các lưu ý quan trọng được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 17, 18, 19 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!
| Công thức | Mô tả |
|---|---|
| f'(x) | Đạo hàm của hàm số f(x) |
| lim x->a f(x) | Giới hạn của hàm số f(x) khi x tiến tới a |