Bài 6.12 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tối ưu hóa. Bài tập này đòi hỏi học sinh phải nắm vững các khái niệm về đạo hàm, cực trị và cách xác định điều kiện để bài toán có nghiệm.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải nhanh chóng cho Bài 6.12 trang 19 SGK Toán 11 tập 2, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho a, b, c là các số thực dương và khác 1. So sánh a, b, c và 1 trong mỗi trường hợp sau:
Đề bài
Cho a, b, c là các số thực dương và khác 1. So sánh a, b, c và 1 trong mỗi trường hợp sau:
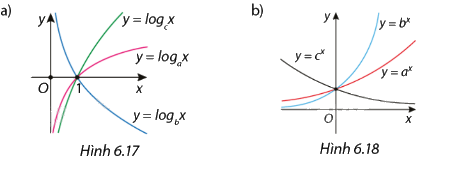
Phương pháp giải - Xem chi tiết
a) Hàm số \(y = {\log _a}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) khi a > 1 và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) khi 0 < a < 1.
b) Hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) khi a > 1 và nghịch biến trên \(\mathbb{R}\) khi 0 < a < 1.
Lời giải chi tiết
a) Ta thấy hàm số \(y = {\log _a}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) nên a > 1
Ta thấy hàm số \(y = {\log _b}x\) nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) 0 < b < 1
Ta thấy hàm số \(y = {\log _c}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) c > 1
b) Ta thấy hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) nên a > 1
Ta thấy hàm số \(y = {b^x}\) đồng biến trên \(\mathbb{R}\) nên b > 1
Ta thấy hàm số \(y = {c^x}\) nghịch biến trên \(\mathbb{R}\) nên 0 < c < 1
Bài 6.12 trang 19 SGK Toán 11 tập 2 thường xoay quanh các bài toán tối ưu hóa, ví dụ như tìm kích thước của một hình hộp chữ nhật để có thể tích lớn nhất với một diện tích bề mặt cho trước, hoặc tìm giá trị của một biến số để một hàm số đạt giá trị lớn nhất hoặc nhỏ nhất.
Giả sử chúng ta có bài toán sau: Một người nông dân muốn xây một chuồng trại hình chữ nhật có diện tích 100m2. Hỏi người nông dân cần xây chuồng trại với kích thước như thế nào để sử dụng ít vật liệu nhất?
Giải:
Khi giải các bài toán tối ưu hóa, cần chú ý đến miền xác định của hàm số và kiểm tra điều kiện của điểm cực trị. Đôi khi, giá trị lớn nhất hoặc nhỏ nhất của hàm số không đạt được tại các điểm cực trị mà tại các điểm biên của miền xác định.
Đạo hàm là một công cụ mạnh mẽ để giải quyết các bài toán tối ưu hóa trong nhiều lĩnh vực khác nhau, như kinh tế, kỹ thuật, vật lý và hóa học. Ví dụ, trong kinh tế, đạo hàm được sử dụng để tìm mức sản lượng tối ưu để đạt lợi nhuận tối đa. Trong kỹ thuật, đạo hàm được sử dụng để thiết kế các cấu trúc có độ bền cao nhất với chi phí thấp nhất.
Để củng cố kiến thức về bài toán tối ưu hóa, bạn có thể luyện tập thêm các bài tập sau:
Bài 6.12 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về ứng dụng của đạo hàm trong việc giải quyết các bài toán tối ưu hóa. Bằng cách nắm vững các bước giải và luyện tập thường xuyên, bạn sẽ có thể tự tin giải quyết các bài toán tương tự trong các kỳ thi và trong thực tế.