Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 62, 63, 64 của sách giáo khoa Toán 11 tập 1.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập. Hãy cùng khám phá và chinh phục những bài toán này nhé!
Cho dãy số chính phương (({u_n})) với ({u_n} = {n^2})
Cho dãy số chính phương (\({u_n}\)) với \({u_n} = {n^2}\)
a, Viết các số hạng tương ứng của dãy số (\({u_n}\)) trong bảng sau:
b, Từ kết quả thu được, nhận xét về giá trị \({u_n}\) khi n tăng lên vô hạn.
c, Từ số hạng thứ mấy thì mọi số hạng \({u_n}\) đều thỏa mãn \({u_n} > 10000000000\)?
Phương pháp giải:
a, Thay các giá trị của n=1,2,3,… để được các giá trị của \({u_n}\) tương ứng.
b, Khi n tăng vô hạn \({u_n} = {n^2}\) cũng tăng lên vô hạn
c, Giá trị 10000000000 ứng với \({u_{100000}}\)
Với các giá trị n>100000 thỏa mãn \({u_n} > 10000000000\)
Lời giải chi tiết:
a, Ta có: \({u_1} = {1^2} = 1;{u_2} = {2^2} = 4;{u_3} = {3^2} = 9;{u_4} = {4^2} = 16\)
\({u_5} = {5^2} = 25;{u_6} = {6^2} = 36;{u_7} = {7^2} = 49;{u_8} = {8^2} = 64\)
\({u_{1000}} = {1000^2} = 1000000\)

b, Từ kết quả câu a ta thấy khi n tăng lên vô hạn thì giá trị \({u_n} = {n^2}\) cũng tăng lên vô hạn.
c, Ta có; \({u_{100000}} = 10000000000\).
Để \({u_n} > 10000000000\) thì n > 100000.
Tìm \(\lim ({2^n}{.3^n}{.4^n})\).
Phương pháp giải:
Áp dụng lim \({q^n} = + \infty \) với q > 1.
Lời giải chi tiết:
Ta có: \(\lim ({2^n}{.3^n}{.4^n}) = \lim ({12^n}) = + \infty \).
Một nhà thầu nhận được hợp đồng sơn màu trang trí một bức tường hình vuông màu trắng kích thước 4m x 4m của một trường mẫu giáo. Hai điều kiện của hợp đồng như sau:
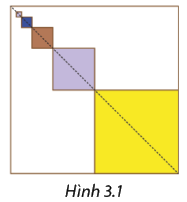
a, Các hình vuông cần sơn màu như hình 3.1. Hình vuông lớn nhất có diện tích bằng một phần tư diện tích bức tường được sơn màu tùy ý khác màu trắng. Mỗi hình vuông tiếp theo có diện tích bằng một phần tư diện tích hình vuông trước nó, được sơn màu khác với hình vuông trước đó và màu trắng;
b, Một phần ba bức tường phải được sơn màu.
Sau khi xem các điều kiện của hợp đồng thì nhà thầu từ chối vì cho rằng không thể thực hiện theo yêu cầu của nhà trường. Hãy giải thích lí do vì sao họ từ chối hợp đồng.

Phương pháp giải:
Diện tích các hình vuông cần sơn là một cấp số nhân lùi vô hạn với q=\(\frac{1}{4}\).
Tổng diện tích các hình vuông cần sơn là tổng của cấp số nhân lùi vô hạn với \({u_1} = 4\) và q=\(\frac{1}{4}\).
Áp dụng công thức tính tổng cấp số nhân lùi vô hạn :
lim\({S_n} = \)\( = \frac{{{u_1}}}{{1 - q}}\).
Lời giải chi tiết:
Vì diện tích hình vuông sau bằng một phần tư diện tích hình vuông trước đó nên diện tích các hình vuông cần sơn là một cấp số nhân lùi vô hạn với công bội q=\(\frac{1}{4}\).
Diện tích hình vuông lớn nhất bằng một phần tư diện tích bức tường nên diện tích hình vuông thứ nhất là: \({u_1} = \frac{1}{4}.4.4 = 4\)(\({m^2}\)).
Tổng diện tích các hình vuông cần được sơn là một cấp số nhân lùi vô hạn với \({u_1} = 4\) và q=\(\frac{1}{4}\) ta có:
S= \({u_1} + {u_2} + ... + {u_n} + ...\)=lim\({S_n} = \)\( = \frac{{{u_1}}}{{1 - q}} = \frac{4}{{1 - \frac{1}{4}}} = \frac{4}{{\frac{3}{4}}} = \frac{{16}}{3}\).
\( \Rightarrow \)lim \({S_n}\) bằng một phần ba diện tích của bức tường
Như vậy, không tìm đươc giá trị của n để thỏa mãn điều kiện b của nhà trường. Do đó, nhà thầu từ chối hợp đồng.
Mục 2 của SGK Toán 11 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết cơ bản, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề sẽ giúp các em tiếp cận bài toán một cách logic và tìm ra lời giải chính xác.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập 1 liên quan đến giới hạn). Để giải bài tập này, ta cần...
Bài tập này tập trung vào... (giả sử bài tập 2 liên quan đến đạo hàm). Lời giải chi tiết như sau:
Ta có hàm số f(x) = ... Để tìm đạo hàm f'(x), ta sử dụng quy tắc...
f'(x) = ...
Bài tập này yêu cầu học sinh... (giả sử bài tập 3 liên quan đến ứng dụng đạo hàm). Để giải quyết bài toán này, ta cần:
Trong mục 2, học sinh có thể gặp các dạng bài tập sau:
Để giải bài tập Toán 11 tập 1 một cách hiệu quả, các em nên:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 62, 63, 64 SGK Toán 11 tập 1. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Chủ đề | Độ khó |
|---|---|---|
| Bài tập 1 | Giới hạn | Dễ |
| Bài tập 2 | Đạo hàm | Trung bình |
| Bài tập 3 | Ứng dụng đạo hàm | Khó |