Chào mừng bạn đến với bài học về Lý thuyết Giới hạn của hàm số, một trong những chủ đề quan trọng nhất của chương trình Toán 11 theo sách giáo khoa. Bài học này sẽ cung cấp cho bạn kiến thức cơ bản và nâng cao về giới hạn, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn trải nghiệm học tập trực tuyến tốt nhất với các bài giảng được trình bày rõ ràng, dễ hiểu và nhiều bài tập thực hành đa dạng.
I. Giới hạn của hàm số tại một điểm
I. Giới hạn của hàm số tại một điểm
1. Giới hạn hữu hạn của hàm số tại một điểm
Cho điểm \({x_0}\) thuộc khoảng K và hàm số \(y = f(x)\) xác định trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(y = f(x)\) có giới hạn hữu hạn là số L khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to L\)
Kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) hay \(f(x) \to L\), khi \({x_n} \to {x_0}\).
2. Định lí về giới hạn hữu hạn của hàm số
a, Cho \(y = f(x)\) và \(y = g(x)\) là các hàm số xác định trên \(K\backslash \left\{ {{x_0}} \right\}\)
Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g(x) = M\), trong đó M, L là các số thực thì:
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)\)
b, Nếu \(f(x) \ge 0\)với mọi \(x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) thì \(L \ge 0\) và \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \).
3. Giới hạn vô cực
Cho điểm \({x_0}\)thuộc khoảng K và hàm số \(y = f(x)\) xác định trên K hoặc \(K\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(f(x)\) có giới hạn là \( + \infty \)(hoặc \( - \infty \) ) khi \(x\) dần tới \({x_0}\) nếu với mọi dãy số \(\left( {{x_n}} \right)\), \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) mà \(\lim {x_n} = {x_0}\), ta đều có \(\lim f\left( {{x_n}} \right) = + \infty \) (hoặc \(\lim f\left( {{x_n}} \right) = - \infty \) kí hiệu kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = + \infty \) hoặc \(f(x) \to + \infty \) khi \(x \to {x_0}\) (tương tự kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = - \infty \) hoặc \(f(x) \to - \infty \) khi \(x \to {x_0}\) ).
II. Giới hạn một phía
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {{x_0};b} \right)\).
Ta nói \(y = f(x)\) có giới hạn bên phải là số L khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì,\({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\).
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;{x_0}} \right)\).
Ta nói \(y = f(x)\) có giới hạn bên phải là số L khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì,\(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L\).
*Định lí:
\(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\)
III. Giới hạn của hàm số tại vô cực
1. Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to + \infty \) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì \({x_n} > a\) và \({x_n} \to + \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to + \infty \).
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( { - \infty ;a} \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to - \infty \) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì \({x_n} < a\) và \({x_n} \to - \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to - \infty \).
* Nhận xét:
\(\mathop {\lim }\limits_{x \to \pm \infty } c = c,\)\(\mathop {\lim }\limits_{x \to \pm \infty } (\frac{c}{{{x^k}}}) = 0\)
2. Giới hạn vô cực của hàm số tại vô cực
a, Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a; + \infty } \right)\).
Ta nói hàm số \(f(x)\) có giới hạn là \( + \infty \) khi \(x \to + \infty \) nếu với dãy số \(\left( {{x_n}} \right),{x_n} > a\)và \(\lim {x_n} = + \infty \), ta đều có \(\lim f\left( {{x_n}} \right) = + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \) hoặc \(f(x) \to + \infty \) khi \(x \to + \infty \) .
b, Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( { - \infty ;a} \right)\).
Ta nói hàm số \(f(x)\)có giới hạn là \( + \infty \) khi \(x \to - \infty \) nếu với dãy số \(\left( {{x_n}} \right),{x_n} < a\)và \(\lim {x_n} = - \infty \), ta đều có \(\lim f\left( {{x_n}} \right) = + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty \) hoặc \(f(x) \to + \infty \) khi \(x \to - \infty \)
Từ hai định nghĩa trên, ta có định nghĩa \(f(x) \to - \infty \) khi \(x \to + \infty \) (hay \(x \to - \infty \)) như sau:
c, \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \left[ { - f(x)} \right] = + \infty \)
d, \(\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty \Leftrightarrow \mathop {\lim }\limits_{x \to - \infty } \left[ { - f(x)} \right] = + \infty \)
* Chú ý:
3. Quy tắc tìm giới hạn của tích và thương tại vô cực
*Giới hạn của tích\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x).g(x)} \right]\)

*Giới hạn của thương \(\frac{{f(x)}}{{g(x)}}\)

Các quy tắc trên vẫn đúng khi thay \( + \infty \) thành \( - \infty \) (\({x_0}^ - \)hoặc \({x_0}^ + \))
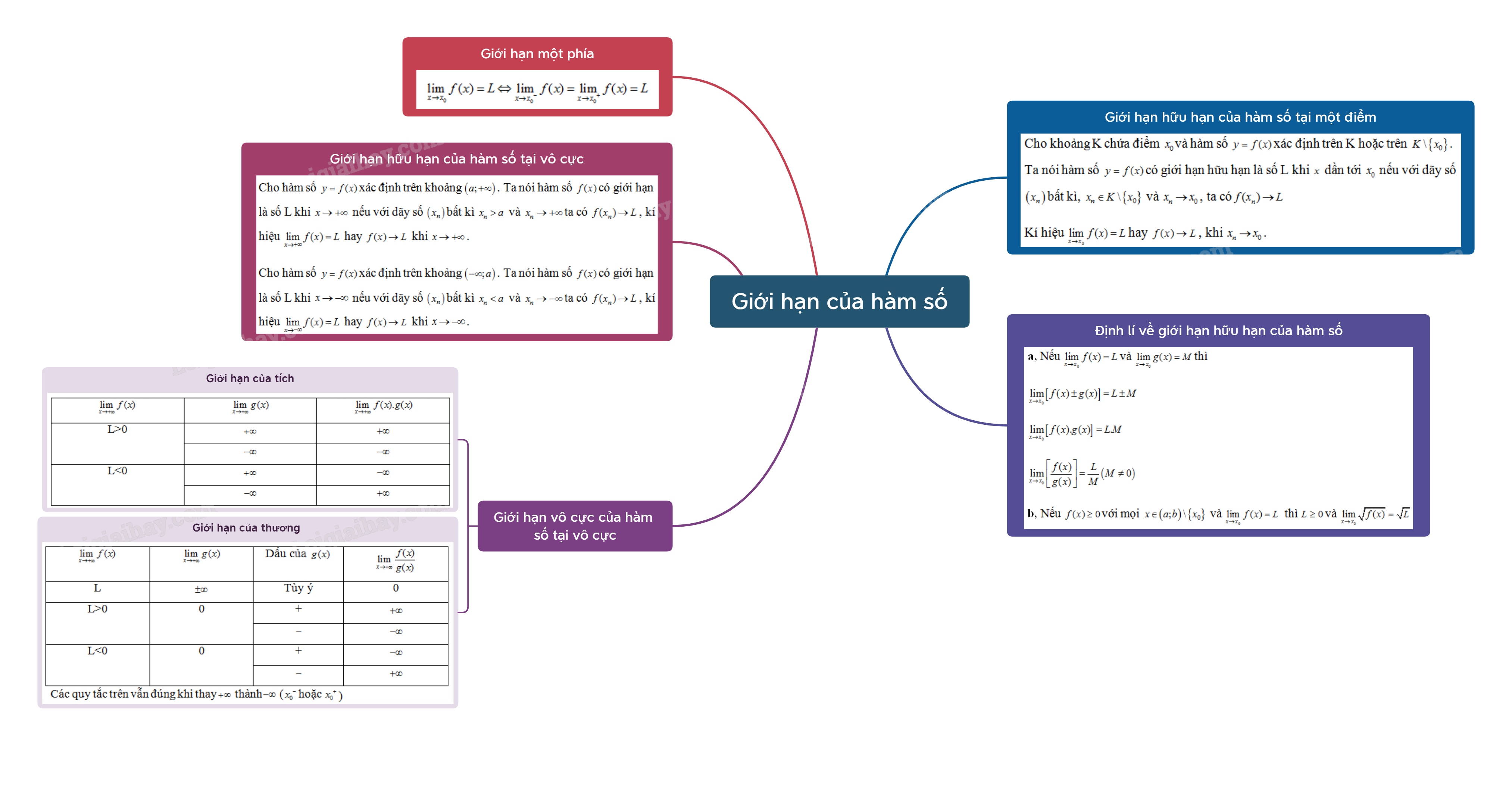
Giới hạn của hàm số là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu sự biến đổi của hàm số khi biến số tiến tới một giá trị nhất định. Trong chương trình Toán 11, học sinh sẽ được làm quen với khái niệm này thông qua sách giáo khoa và các bài tập thực hành.
Giới hạn của hàm số f(x) khi x tiến tới a được ký hiệu là limx→a f(x) = L, nếu với mọi số dương ε (epsilon) nhỏ tùy ý, tồn tại một số dương δ (delta) sao cho nếu 0 < |x - a| < δ thì |f(x) - L| < ε. Nói một cách đơn giản, khi x tiến gần a, giá trị của f(x) tiến gần L.
Việc nắm vững các tính chất của giới hạn sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và hiệu quả:
Có một số dạng giới hạn thường gặp trong chương trình Toán 11, bao gồm:
Ví dụ 1: Tính limx→2 (x2 - 4) / (x - 2)
Giải: limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 4
Ví dụ 2: Tính limx→0 sin(3x) / x
Giải: limx→0 sin(3x) / x = 3 * limx→0 sin(3x) / (3x) = 3 * 1 = 3
Khái niệm giới hạn có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Giới hạn của hàm số. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.