Chào mừng bạn đến với bài học về Lý thuyết Khoảng cách trong chương trình SGK Toán 11. Đây là một phần kiến thức quan trọng, giúp bạn hiểu rõ hơn về hình học không gian và ứng dụng trong giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập vận dụng đa dạng, giúp bạn nắm vững kiến thức một cách hiệu quả nhất.
A. Lý thuyết 1. Khoảng cách từ một điểm đến một đường thẳng
A. Lý thuyết
1. Khoảng cách từ một điểm đến một đường thẳng
| Cho điểm O không thuộc đường thẳng a. H là hình chiếu của O trên a. Độ dài OH được gọi là khoảng cách từ điểm O đến đường thẳng a, kí hiệu d(O,a). |
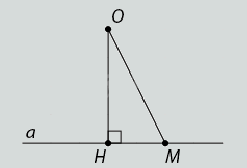
Lưu ý:
- d(O,a) là nhỏ nhất so với khoảng cách từ O đến mọi điểm thuộc a.
- d(O,a) = 0 khi và chỉ khi O thuộc a.
2. Khoảng cách giữa hai đường thẳng song song, giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
a) Khoảng cách giữa hai đường thẳng song song
| Khoảng cách giữa hai đường thẳng song song a, b là khoảng cách từ một điểm bất kì trên đường thẳng a đến đường thẳng b, kí hiệu là d(a,b). |
b) Khoảng cách giữa đường thẳng và mặt phẳng song song
| Khoảng cách giữa đường thẳng a và mặt phẳng \((\alpha )\) song song với a là khoảng cách từ một điểm A bất kì thuộc a đến \((\alpha )\). Khoảng cách giữa a và \((\alpha )\) được kí hiệu là \(d(a,(\alpha ))\). |
c) Khoảng cách giữa hai mặt phẳng song song
| Khoảng cách giữa hai mặt phẳng song song \((\alpha )\) và \((\beta )\) là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia, kí hiệu là \(d((\alpha ),(\beta ))\). |
Lưu ý: \(d((\alpha ),(\beta )) = d(M,(\beta ))\) với \(M \in (\alpha )\) và \(d((\alpha ),(\beta )) = d(M',(\alpha ))\), với \(M' \in (\beta )\).
3. Đường vuông góc chung và khoảng cách giữa hai đường thẳng chéo nhau
a) Khái niệm
Đường thẳng Δ cắt hai đường thẳng chéo nhau a, b và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung của a và b. Nếu đường vuông góc chung Δ cắt hai đường thẳng chéo nhau a, b lần lượt tại M, N thì độ dài đoạn MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b, kí hiệu d(a,b). |
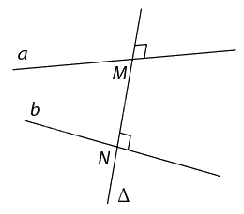
b) Tính chất
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó chứa đường thẳng còn lại. - Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó. |
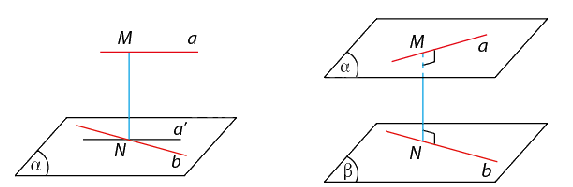
Lưu ý: Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách nhỏ nhất trong các khoảng cách giữa hai điểm bất kì lần lượt nằm trên hai đường thẳng đó.
B. Bài tập
Bài 1: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính khoảng cách từ điểm B đến đường chéo AC’.
Giải:
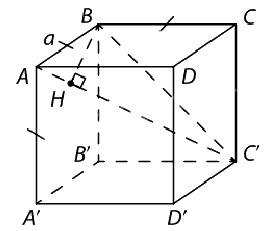
Khoảng cách từ B đến AC’ là chiều cao BH của tam giác BAC’.
Ta có:
ABCD.A’B’C’D’ là hình lập phương nên \(AB \bot (BB'C'C) \Rightarrow AB \bot BC'\); hay tam giác ABC’ vuông tại B.
AB = a, \(BC' = \sqrt 2 a\) (BB’C’C là hình vuông cạnh a) nên \(AC' = \sqrt 3 a\) (đường chéo hình lập phương cạnh a).
\(BA.BC' = BH.AC = 2{S_{\Delta ABC}}\). Suy ra \(BH = \frac{{\sqrt 6 }}{3}a\).
Vậy \(d(B;AC') = BH = \frac{{\sqrt 6 }}{3}a\).
Bài 2: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng các từ S đến mặt phẳng (ABCD).
Giải:
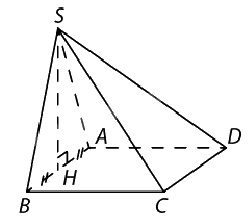
Hai mặt phẳng (SAB) và (ABCD) vuông góc nhau theo giao tuyến AB.
Gọi H là trung điểm của AB thì \(SH \bot AB\). Suy ra \(SH \bot (ABCD)\) tại H.
Vậy \(d(S,ABCD) = SH = \frac{{\sqrt 3 }}{2}a\) (chiều cao của tam giác đều cạnh a).
Bài 3: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính khoảng cách giữa hai đường thẳng BC’ và AD’.
Giải:
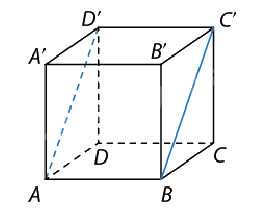
Do ABCD.A’B’C’D’ là hình lập phương nên ABC’D’ là hình chữ nhật.
Do đó BC’ // AD’.
Vậy \(d(BC',AD') = d(A,BC') = AB = a\).
Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết \(SA \bot (ABCD)\) và SA = 2a. Tính khoảng cách giữa đường thẳng AB và mặt phẳng (SCD).
Giải:
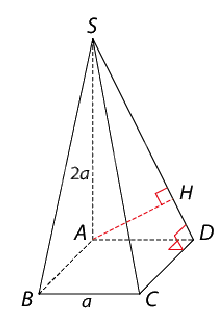
AB // CD, \(CD \subset (SCD)\) nên AB // (SCD).
Vậy \(d(AB,(SCD)) = d(A,(SCD))\).
Ta có \(CD \bot SA\) và \(CD \bot AD\) nên \(CD \bot (SAD)\). Vậy \((SAD) \bot (SCD)\).
Mà \((SAD) \cap (SCD) = SD\) nên gọi H là hình chiếu của A trên SD thì \(AH \bot (SCD)\) và \(d(A,(SCD)) = AH\).
Xét tam giác SAD vuông tại A có SA = 2a, AD = a nên \(S{D^2} = A{D^2} + S{A^2} = 5{a^2}\) hay \(SD = \sqrt 5 a\).
Suy ra \(AH.SD = SA.AD \Rightarrow AH = \frac{{SA.AD}}{{SD}} = \frac{{2\sqrt 5 }}{5}a\).
Vậy \(d(AB,(SCD)) = \frac{{2\sqrt 5 }}{5}a\).
Bài 5: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, A’ cách đều A, B, C và AA’ = 2a. Tính khoảng cách giữa hai đáy của hình lăng trụ này.
Giải:
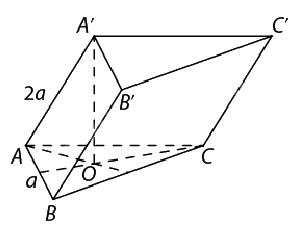
Do (ABC) // (A’B’C’) nên \(d((ABC),(A'B'C')) = d(A',(ABC))\).
Vì tam giác ABC đều và AA’ = A’B = A’C nên A’.ABC là hình chóp tam giác đều.
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Ta có: A’.ABC là hình chóp đều nên A’O vuông góc với (ABC) tại O. Vậy d(A’,(ABC)) = A’O.
Ta có \(A'O = \sqrt {A'{A^2} - A{O^2}} = \frac{{\sqrt {33} }}{3}a\).
Vậy \(d((ABC),(A'B'C')) = \frac{{\sqrt {33} }}{3}a\).
Bài 6: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính khoảng cách giữa các cặp đường thẳng sau:
a) BB’ và AC.
b) BB’ và A’C.
c) AC và B’D’.
Giải:
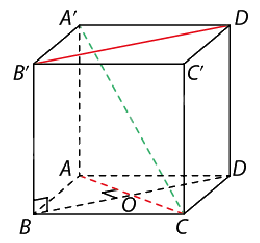
a) Gọi O là tâm hình vuông ABCD. Ta có:
\(BO \bot AC\) (ABCD là hình vuông).
\(BO \bot BB'\) (do ABCD.A’B’C’D’ là hình lập phương nên \(BB' \bot (ABCD)\)); BO cắt AC, BB’ lần lượt tại O, B.
Suy ra BO là đoạn vuông góc chung của hai đường thẳng BB’ và AC.
Mà ABCD là hình vuông cạnh a, nên \(BO = \frac{{\sqrt 2 }}{2}a\).
Vậy khoảng cách giữa hai đường thẳng chéo nhau BB’ và AC là \(BO = \frac{{\sqrt 2 }}{2}a\).
b) Ta có: BB’ // AA’, suy ra (ACA’) chứa AC và song song với BB’.
Suy ra \(d(BB';AC) = d(BB';(ACA')) = d(B;(ACA')) = BO = \frac{{\sqrt 2 }}{2}a\).
c) Ta có AC và B’D’ lần lượt nằm trên hai mặt phẳng song song nhau là (ABCD) và (A’B’C’D’) nên \(d(AC,B'D') = d((ABCD),(A'B'C'D')) = AA' = a\).
Trong chương trình Toán 11, phần Lý thuyết Khoảng cách đóng vai trò then chốt trong việc xây dựng nền tảng vững chắc cho các kiến thức hình học không gian. Nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là bước đệm quan trọng cho các chương trình học nâng cao.
Khoảng cách giữa hai điểm A(xA, yA, zA) và B(xB, yB, zB) trong không gian được tính theo công thức:
d(A, B) = √[(xB - xA)2 + (yB - yA)2 + (zB - zA)2]
Công thức này là mở rộng của công thức tính khoảng cách giữa hai điểm trên mặt phẳng, và là cơ sở để tính toán các khoảng cách khác trong không gian.
Để tính khoảng cách từ điểm M(x0, y0, z0) đến đường thẳng Δ có phương trình tham số:
{ x = x0 + at { y = y0 + bt { z = z0 + ct}
Ta thực hiện các bước sau:
Khoảng cách từ điểm M(x0, y0, z0) đến mặt phẳng (P) có phương trình:
Ax + By + Cz + D = 0
Được tính theo công thức:
d(M, (P)) = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2)
Công thức này là một trong những công thức quan trọng nhất trong hình học không gian, được sử dụng rộng rãi trong việc giải các bài toán liên quan đến khoảng cách và vị trí tương đối giữa điểm và mặt phẳng.
Để tính khoảng cách giữa hai đường thẳng Δ1 và Δ2, ta thực hiện các bước sau:
Lý thuyết Khoảng cách có nhiều ứng dụng trong thực tế, bao gồm:
Để củng cố kiến thức về Lý thuyết Khoảng cách, bạn có thể thực hành giải các bài tập sau:
| Bài tập | Mô tả |
|---|---|
| Bài 1 | Tính khoảng cách giữa hai điểm A(1, 2, 3) và B(4, 5, 6). |
| Bài 2 | Tính khoảng cách từ điểm M(0, 0, 0) đến đường thẳng x = t, y = t, z = t. |
| Bài 3 | Tính khoảng cách từ điểm N(1, 1, 1) đến mặt phẳng x + y + z - 1 = 0. |
Lý thuyết Khoảng cách là một phần kiến thức quan trọng trong chương trình Toán 11. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả và tự tin. Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để đạt được kết quả tốt nhất.