Chào mừng bạn đến với bài học về lý thuyết thể tích khối lăng trụ, khối chóp và khối chóp cụt đều, thuộc chương trình SGK Toán 11. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và công thức quan trọng để giải quyết các bài toán liên quan đến thể tích trong không gian.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất và các công thức tính thể tích của từng loại khối đa diện này. Đồng thời, bài học cũng sẽ giới thiệu các phương pháp áp dụng lý thuyết vào giải bài tập một cách hiệu quả.
A. Lý thuyết 1. Thể tích khối lăng trụ
A. Lý thuyết
1. Thể tích khối lăng trụ
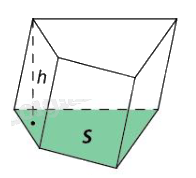
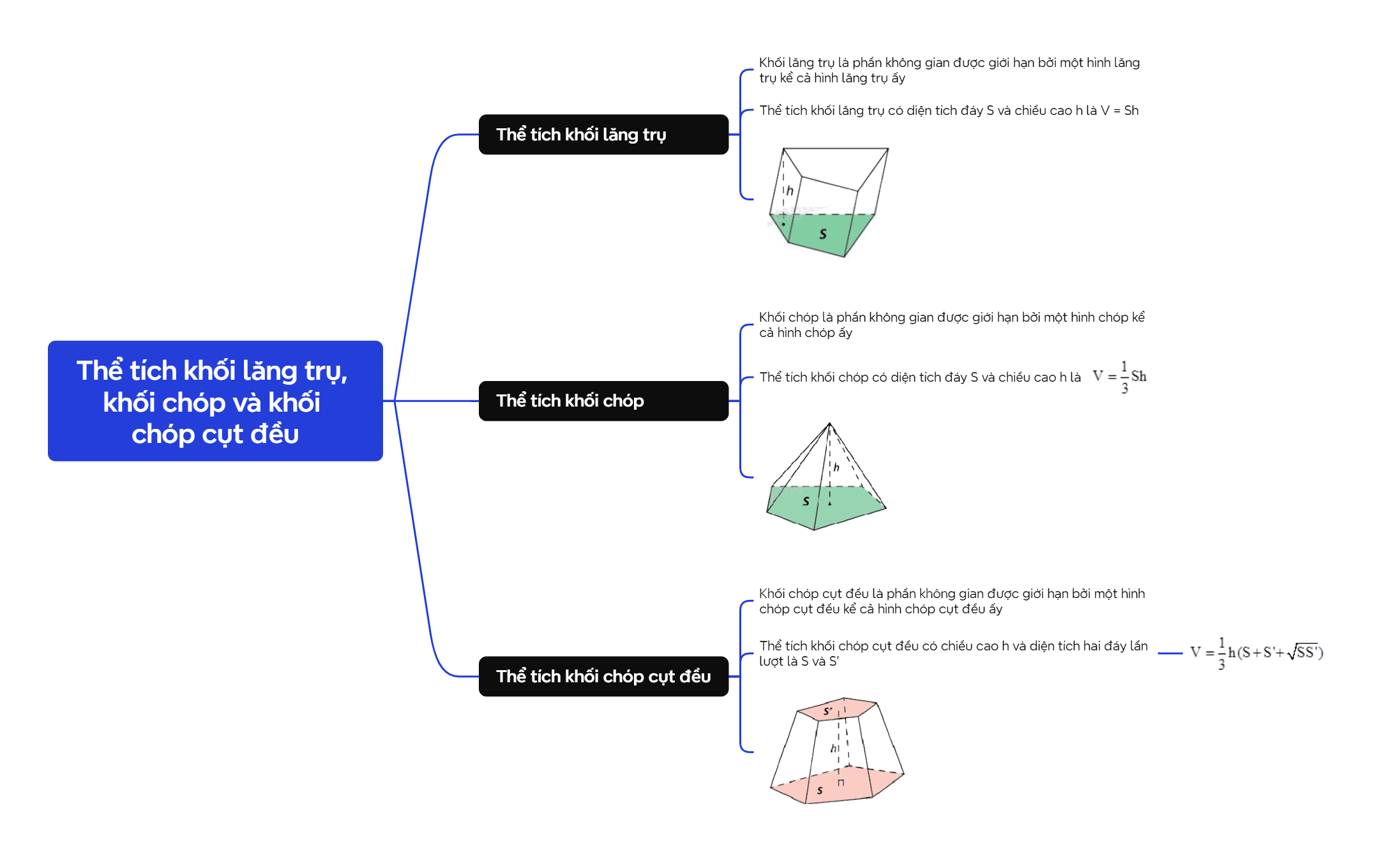
| Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy. |
Lưu ý: Tên của khối lăng trụ được đặt theo tên của hình lăng trụ giới hạn nó.

| Thể tích khối lăng trụ có diện tích đáy S và chiều cao h là V = Sh. |
2. Thể tích khối chóp
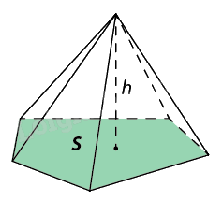
| Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy. |
Lưu ý: Tên của khối chóp được đặt theo tên của hình chóp giới hạn nó.
| Thể tích khối chóp có diện tích đáy S và chiều cao h là \(V = \frac{1}{3}Sh\). |
3. Thể tích khối chóp cụt đều
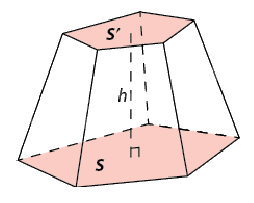
| Khối chóp cụt đều là phần không gian được giới hạn bởi một hình chóp cụt đều kể cả hình chóp cụt đều ấy. |
Lưu ý: Tên của khối chóp cụt dều được đặt theo tên của hình chóp cụt đều giới hạn nó.
Thể tích khối chóp cụt đều có chiều cao h và diện tích hai đáy lần lượt là S và S’: \(V = \frac{1}{3}h(S + S' + \sqrt {SS'} )\). |
B. Bài tập
Bài 1: Cho hình lăng trụ ABCD.A’B’C’D’ có cạnh bên bằng 2a, đáy là hình vuông ABCD cạnh a. Hình chiếu của A’ trên mặt phẳng (ABCD) là giao điểm O của AC và BD. Tính thể tích khối lăng trụ này.
Giải:
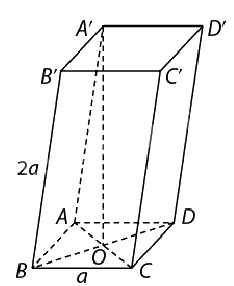
ABCD là hình vuông cạnh a nên diện tích hình vuông ABCD là \({S_{ABCD}} = {a^2}\).
Hình chiếu của A’ trên (ABCD) là O nên chiều cao hình lăng trụ là A’O.
Ta có: \(A'{O^2} = A'{A^2} - A{O^2} = 4{a^2} - {\left( {\frac{{\sqrt 2 }}{2}a} \right)^2} = \frac{{14{a^2}}}{4} \Rightarrow A'O = \frac{{\sqrt {14} }}{2}a\).
Vậy thể tích khối lăng trụ đã cho là \(V = A'O.{S_{ABCD}} = \frac{{\sqrt {14} }}{2}{a^3}\).
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với mặt phẳng đáy và SA = a. Biết rằng \(AB = \sqrt 2 a\), \(AC = \sqrt 3 a\). Tính thể tích của khối chóp này.
Giải:
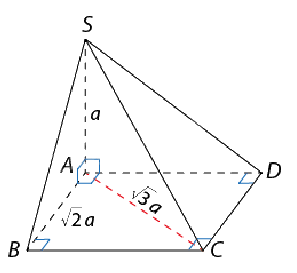
Ta có A là hình chiếu của A trên mặt đáy (ABCD) nên chiều cao của hình chóp S.ABCD là SA = a.
Vì ABCD là hình chữ nhật nên \(B{C^2} = A{C^2} - A{B^2} = {a^2} \Rightarrow BC = a\) nên diện tích ABCD là \({S_{ABCD}} = AB.BC = \sqrt 2 {a^2}\).
Vậy thể tích khối chóp S.ABCD là \({V_{S.ABCD}} = \frac{1}{3}SA.{S_{ACBD}} = \frac{{\sqrt 2 }}{3}{a^3}\).
Bài 3: Một phòng ngủ ngoài trời có hình dạng hình chóp cụt đều, cạnh đáy lớn bằng 150 cm, cạnh đáy nhỏ bằng 120 cm, chiều cao 180 cm. Tính thể tích phần không gian bên trong phòng ngủ.

Giải:
Cạnh đáy lớn bằng 150 cm nên diện tích đáy lớn là \(S = {150^2} = 22500\) \((c{m^2})\).
Cạnh đáy nhỏ bằng 120 cm nên diện tích đáy nhỏ là \(S' = {120^2} = 14400\) \((c{m^2})\).
Chiều cao chóp cụt là h = 180 cm.
Thể tích phòng ngủ là \(V = \frac{1}{3}h(S + S' + \sqrt {SS'} ) = 3294000\) \((c{m^3})\).
Trong chương trình Toán 11, phần hình học không gian đóng vai trò quan trọng, và việc nắm vững lý thuyết về thể tích các khối đa diện là nền tảng để giải quyết các bài toán phức tạp hơn. Bài viết này sẽ trình bày chi tiết lý thuyết về thể tích khối lăng trụ, khối chóp và khối chóp cụt đều, dựa trên nội dung SGK Toán 11.
1. Định nghĩa: Khối lăng trụ là một khối đa diện được tạo thành bởi hai mặt đáy song song và bằng nhau, và các mặt bên là các hình bình hành.
2. Công thức tính thể tích: V = B.h, trong đó:
3. Các trường hợp đặc biệt:
1. Định nghĩa: Khối chóp là một khối đa diện được tạo thành bởi một mặt đáy là một đa giác, và các mặt bên là các tam giác có chung đỉnh.
2. Công thức tính thể tích: V = (1/3).B.h, trong đó:
3. Các trường hợp đặc biệt:
1. Định nghĩa: Khối chóp cụt đều là phần của khối chóp bị cắt bởi một mặt phẳng song song với mặt đáy.
2. Công thức tính thể tích: V = (1/3).h.(B1 + B2 + √(B1.B2)), trong đó:
Ví dụ 1: Tính thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng 5cm và chiều cao bằng 8cm.
Giải:
Diện tích mặt đáy (tam giác đều) là: B = (√3/4).a2 = (√3/4).52 = (25√3)/4 cm2
Thể tích khối lăng trụ là: V = B.h = ((25√3)/4).8 = 50√3 cm3
Ví dụ 2: Tính thể tích của khối chóp tứ giác đều có cạnh đáy bằng 6cm và chiều cao bằng 10cm.
Giải:
Diện tích mặt đáy (hình vuông) là: B = a2 = 62 = 36 cm2
Thể tích khối chóp là: V = (1/3).B.h = (1/3).36.10 = 120 cm3
Khi tính thể tích các khối đa diện, cần chú ý đến đơn vị đo. Đảm bảo rằng tất cả các kích thước đều được biểu diễn bằng cùng một đơn vị đo trước khi thực hiện phép tính.
Ngoài ra, việc hiểu rõ định nghĩa và tính chất của từng loại khối đa diện là rất quan trọng để áp dụng đúng công thức tính thể tích.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết thể tích khối lăng trụ, khối chóp và khối chóp cụt đều. Chúc bạn học tập tốt!