Bài 5.19 thuộc chương trình Toán 11 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các công thức đạo hàm cơ bản và kỹ năng giải phương trình, bất phương trình.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Một công ty giống cây trồng đã cho trồng thử nghiệm hai giống lúa vụ đông xuân ở một số địa phương, với điều kiện thổ nhưỡng và chế độ chăm sóc như nhau. Cuối vụ, công ty tìm hiểu năng suất mỗi giống lúa trên những thửa ruộng đã trồng thí điểm và thu được dữ liệu ở bảng sau:
Đề bài
Một công ty giống cây trồng đã cho trồng thử nghiệm hai giống lúa vụ đông xuân ở một số địa phương, với điều kiện thổ nhưỡng và chế độ chăm sóc như nhau. Cuối vụ, công ty tìm hiểu năng suất mỗi giống lúa trên những thửa ruộng đã trồng thí điểm và thu được dữ liệu ở bảng sau:

Trong vai nhà nghiên cứu, hãy phân tích dữ liệu về năng suất mỗi giống lúa và quyết định nên triển khai trồng đại trà giống lúa nào. Giải thích sự lựa chọn đó.
Phương pháp giải - Xem chi tiết
Phân tích dữ liệu về năng suất bằng cách đi tính trung bình, trung vị, mốt của mỗi giống lúa.
+) \(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
+) Trung vị \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\) trong đó \({L_m},{n_m},h\) lần lượt là đầu mút trái, tần số và độ dài của nhóm chứa trung vị. \(T\) là tần số tích lũy của nhóm ngay trước nhóm chứa trung vị.
Nhóm chứa trung vị của mẫu số liệu là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\) , trong đó \(N\) là cỡ mẫu.
+) Công thức tìm mốt của mẫu số liệu ghép nhóm là \({M_0} = {L_m} + \frac{a}{{a + b}}.h\)
Lời giải chi tiết
+) Tính trung bình
Ta có bảng sau
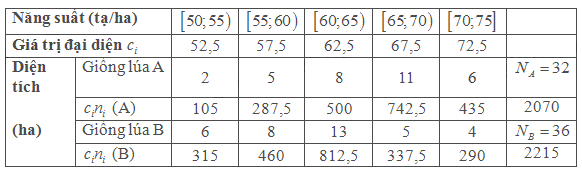
Áp dụng công thức trung bình ta có
\(\overline {{x_A}} = \frac{{2070}}{{32}} \approx 64,7\); \(\overline {{x_B}} = \frac{{2215}}{{36}} \approx 61,5\)
+) Tính trung vị
Bảng tần số tích lũy sau
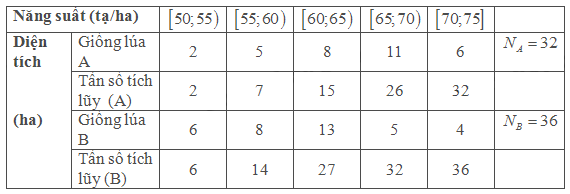
* Với giống lúa A có \(\frac{{{N_A}}}{2} = \frac{{32}}{2} = 16\). Do đó nhóm có tần số tích lũy lớn hơn hoặc bằng 16 là nhóm \(\left[ {65;70} \right)\).
Ta có \({L_m} = 65;h = 70 - 65 = 5;{n_m} = 11\), \(T = 15\).
Áp dụng công thức tính \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 65 + \frac{{16 - 15}}{{11}}.5 \approx 65,5\)
* Với giống lúa \(B\) có \(\frac{{{N_B}}}{2} = \frac{{36}}{2} = 18\). Do đó nhóm có tần số tích lũy lớn hơn hoặc bằng 18 là nhóm \(\left[ {60;65} \right)\).
Ta có \({L_m} = 60;h = 65 - 60 = 5;{n_m} = 13;T = 14\)
Áp dụng công thức tính \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 60 + \frac{{18 - 14}}{{13}}.5 \approx 61,5\)
+ Tính mốt
* Với giống lúa A thì nhóm chứa mốt là \(\left[ {65;70} \right)\) với tần số \(n = 11\), \(h = 70 - 65 = 5\)
\({L_m} = 65;a = 11 - 8 = 3;b = 11 - 6 = 5;\)
Ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 65 + \frac{3}{{3 + 5}}.5 \approx 66,9\)
* Với giống lúa B thì nhóm chứa mốt là \(\left[ {60;65} \right)\) với tần số \(n = 13;h = 65 - 60 = 5\)
\({L_m} = 60;a = 13 - 8 = 5;b = 13 - 5 = 8\)
Ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 60 + \frac{5}{{5 + 8}}.5 \approx 61,9\)
Dựa vào các dữ liệu về tính trung bình, trung vị và mốt ta nhận thấy giống lúa A đều cho năng suất hơn giống lúa B. Do đó nên triển khai trồng đại trà giống lúa A
Bài 5.19 SGK Toán 11 tập 1 yêu cầu giải một bài toán liên quan đến đạo hàm của hàm số. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài toán: (Giả sử bài toán cụ thể là: Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm y' và xác định các điểm cực trị của hàm số.)
Bước 1: Tính đạo hàm y'
Áp dụng quy tắc tính đạo hàm của tổng và lũy thừa, ta có:
y' = 3x2 - 6x
Bước 2: Tìm các điểm cực trị
Để tìm các điểm cực trị, ta giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Bước 3: Xác định loại cực trị
Ta xét dấu của đạo hàm y' trên các khoảng xác định:
Vậy, hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Kết luận:
Hàm số y = x3 - 3x2 + 2 đạt cực đại tại điểm (0, 2) và cực tiểu tại điểm (2, -2).
Lưu ý:
Trong quá trình giải bài toán, cần chú ý đến các bước tính toán và kiểm tra lại kết quả để đảm bảo tính chính xác. Ngoài ra, cần nắm vững các kiến thức về đạo hàm và ứng dụng của đạo hàm để giải quyết các bài toán tương tự.
Mở rộng:
Bài toán này có thể được mở rộng bằng cách thay đổi hàm số hoặc yêu cầu tìm các điểm uốn của hàm số. Để giải quyết các bài toán mở rộng này, cần nắm vững các kiến thức về đạo hàm bậc hai và ứng dụng của đạo hàm bậc hai.
Ví dụ minh họa:
Xét hàm số y = x4 - 4x3 + 6x2 - 4x + 1. Tìm đạo hàm y' và xác định các điểm cực trị của hàm số.
Giải:
y' = 4x3 - 12x2 + 12x - 4
y' = 4(x3 - 3x2 + 3x - 1)
y' = 4(x - 1)3
Giải phương trình y' = 0, ta được x = 1.
Xét dấu của đạo hàm y' trên các khoảng xác định:
Vậy, hàm số đạt cực tiểu tại x = 1.
Tổng kết:
Bài 5.19 trang 148 SGK Toán 11 tập 1 là một bài toán quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Việc giải bài toán này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải phương trình, bất phương trình. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các bạn học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 11 tập 1.