Chào mừng bạn đến với bài giải Bài 1.3 trang 7 SGK Toán 11 tập 1 trên giaitoan.edu.vn. Bài học này tập trung vào việc xác định tập xác định và tập giá trị của hàm số, một kiến thức nền tảng quan trọng trong chương trình Toán 11.
Chúng tôi cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của bài toán và cách áp dụng các công thức, định lý liên quan.
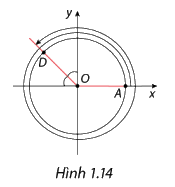
Xác định số đo của góc lượng giác (OA, OD) trong Hình 1.14 theo đơn vị radian và theo đơn vị độ, biết rằng OD là tia phân giác của góc phần tư thứ hai.
Đề bài
Xác định số đo của góc lượng giác (OA, OD) trong Hình 1.14 theo đơn vị radian và theo đơn vị độ, biết rằng OD là tia phân giác của góc phần tư thứ hai.
Phương pháp giải - Xem chi tiết
Xác định tia đầu, tia cuối và chiều quay để tìm được số đo của góc lượng giác.
Lời giải chi tiết
Góc lượng giác có tia đầu OA, tia cuối OD, quay theo chiều tạo nên cung \(\frac{{3\pi }}{4}\) và đi tiếp 2 vòng tròn nữa nên sđ(OA, OD) = \(\frac{{3\pi }}{4} + 2.2\pi = \frac{{19\pi }}{4} = {855^0}\).
Bài 1.3 trang 7 SGK Toán 11 tập 1 yêu cầu học sinh xác định tập xác định và tập giá trị của các hàm số được cho. Đây là một bài tập quan trọng giúp củng cố kiến thức về hàm số, một khái niệm cơ bản trong toán học.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các khái niệm sau:
Để xác định TXĐ, ta cần chú ý đến các điều kiện sau:
Để xác định TGT, ta thường xét các giá trị lớn nhất, nhỏ nhất của hàm số, hoặc sử dụng các phương pháp biến đổi hàm số.
Dưới đây là lời giải chi tiết cho từng câu của Bài 1.3 trang 7 SGK Toán 11 tập 1:
TXĐ: Vì hàm số là hàm số bậc nhất, không có điều kiện gì về x, nên TXĐ là R (tập hợp tất cả các số thực).
TGT: Vì hàm số là hàm số bậc nhất, nó có thể nhận bất kỳ giá trị nào, nên TGT là R.
TXĐ: Vì hàm số là hàm số bậc hai, không có điều kiện gì về x, nên TXĐ là R.
TGT: Vì x2 ≥ 0 với mọi x, nên x2 + 1 ≥ 1. Do đó, TGT là [1; +∞).
TXĐ: Để hàm số có nghĩa, mẫu số phải khác 0, tức là x - 2 ≠ 0, suy ra x ≠ 2. Vậy TXĐ là R \ {2}.
TGT: Vì x ≠ 2, nên 1/(x - 2) có thể nhận bất kỳ giá trị khác 0. Vậy TGT là R \ {0}.
TXĐ: Để căn bậc hai có nghĩa, biểu thức bên trong phải lớn hơn hoặc bằng 0, tức là x - 3 ≥ 0, suy ra x ≥ 3. Vậy TXĐ là [3; +∞).
TGT: Vì x ≥ 3, nên x - 3 ≥ 0, suy ra √(x - 3) ≥ 0. Vậy TGT là [0; +∞).
Để hiểu sâu hơn về tập xác định và tập giá trị của hàm số, bạn có thể làm thêm các bài tập sau:
Bài 1.3 trang 7 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh nắm vững kiến thức về tập xác định và tập giá trị của hàm số. Việc hiểu rõ các khái niệm này là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 11.
Hy vọng với lời giải chi tiết và phân tích chuyên sâu này, bạn đã hiểu rõ cách giải Bài 1.3 trang 7 SGK Toán 11 tập 1. Chúc bạn học tốt!