Bài 8.31 trang 83 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề cụ thể.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho Bài 8.31 trang 83 SGK Toán 11 tập 2, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập.
Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình chữ nhật, AB = 3a và AD = 4a.
Đề bài
Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình chữ nhật, AB = 3a và AD = 4a. Hình chiếu vuông góc của A’ trên mặt phẳng (ABCD) là trung điểm của AD và AA’ = 4a. Tính thể tích khối hộp này.
Phương pháp giải - Xem chi tiết
Công thức tính thể tích hình hộp: V = S.h với S là diện tích đáy, h là chiều cao.
Lời giải chi tiết
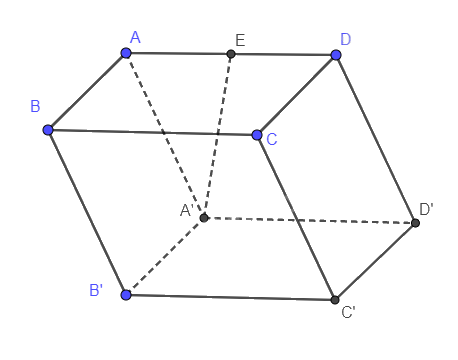
Gọi E là trung điểm của AD nên AE = 2a
\(A'E = \sqrt {AA{'^2} - A{E^2}} = \sqrt {{{\left( {4a} \right)}^2} - {{\left( {2a} \right)}^2}} = 2\sqrt 3 a\)
\(V = S.h = AB.AD.A'E = 3a.4a.2\sqrt 3 a = 24\sqrt 3 {a^3}\)
Bài 8.31 trang 83 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 8.31 trang 83 SGK Toán 11 tập 2 thường yêu cầu học sinh thực hiện các thao tác sau:
Lời giải chi tiết:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu chúng ta khảo sát hàm số y = x3 - 3x2 + 2.
Bước 1: Tính đạo hàm của hàm số:
y' = 3x2 - 6x
Bước 2: Tìm các điểm cực trị của hàm số:
Để tìm các điểm cực trị, chúng ta cần giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2.
Bước 3: Xác định loại cực trị:
Để xác định loại cực trị, chúng ta có thể sử dụng bảng xét dấu của đạo hàm y'.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Từ bảng xét dấu, ta thấy rằng:
Bước 4: Khảo sát sự biến thiên của hàm số:
Dựa vào bảng xét dấu của đạo hàm, ta có thể kết luận rằng:
Kết luận:
Hàm số y = x3 - 3x2 + 2 đạt cực đại tại x = 0 và cực tiểu tại x = 2. Hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2).
Lưu ý:
Khi giải các bài tập về đạo hàm và ứng dụng của đạo hàm, học sinh cần chú ý đến các bước sau:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp học sinh hiểu rõ hơn về cách giải Bài 8.31 trang 83 SGK Toán 11 tập 2 và các bài tập tương tự. Chúc các em học tập tốt!
Việc nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm là rất quan trọng đối với học sinh lớp 11. Nó không chỉ giúp các em giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng để học các môn học khác liên quan đến toán học và khoa học tự nhiên.
Ngoài ra, giaitoan.edu.vn còn cung cấp nhiều tài liệu học tập khác về Toán 11, bao gồm các bài giảng, bài tập trắc nghiệm, đề thi thử và các video hướng dẫn giải bài tập. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu hữu ích khác.