Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 tại giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 2 của chương trình Toán 11 tập 2 thường tập trung vào các kiến thức quan trọng về... (Nội dung cụ thể của Mục 2 sẽ được điền vào đây khi có thông tin chi tiết)
Vẽ hai đường thẳng song song a và b.
Vẽ hai đường thẳng song song a và b.
Trên a, lấy hai điểm phân biệt tùy ý A và A’.
Hãy xác định d(A,b) và d(A’,b) rồi so sánh hai khoảng các này.

Phương pháp giải:
Tứ giác có 2 cặp cạnh song song là hình bình hành. Hình bình hành có 2 cặp cạnh đối song song và bằng nhau.
Lời giải chi tiết:
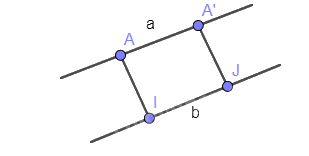
Kẻ AI vuông góc với b, A’J vuông góc với a
Mà a // b nên A’J vuông góc với b. Suy ra AI song song với A’J
Mặt khác, AA’ song song với IJ
Suy ra AA’JI là hình bình hành
Nên AI = A’J
Vậy d(A,b) = d(A’,b).
Cho hình lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC. Mặt phẳng (GA’C’) cắt AB, BC lần lượt tại M, N. Tính diện tích tứ giác A’C’NM.
Phương pháp giải:
Diện tích hình thang: \(S = h.\frac{{a + b}}{2}\)
Với h là đường cao, a là đáy lớn, b là đáy nhỏ.
Lời giải chi tiết:

Kẻ đường thẳng đi qua G và song song với A’C’ cắt AB, AC tại M, N
Suy ra A’C’MN là hình thang
Xét tam giác ABC có: MN // AC (cùng // A’C’) nên MN = \(\frac{2}{3}\)AC \(\frac{2}{3}\)a
Gọi M’ là trung điểm của A’C’, G’ là trọng tâm tam giác A’B’C’
Ta có: GG’ vuông góc với (A’B’C’) nên GG’ vuông góc với A’C’
G’M’ là trung tuyến của A’B’C’ nên G’M’ vuông góc với A’C’ (Vì tam giác A’B’C’ đều)
Suy ra (GG’M’) vuông góc với A’C’
\( \Rightarrow \)GM’ vuông góc với A’C’
Tam giác A’B’C’ đều cạnh a nên B’M’ = \(B'M' = \frac{{\sqrt 3 }}{2}a\)
Suy ra G’M’ = \(G'M' = \frac{{\sqrt 3 }}{6}a\)
Xét tam giác vuông GM’G’ tại M’ có:
\(GM' = \sqrt {GG{'^2} + G'M{'^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{{\sqrt 3 }}{6}a} \right)}^2}} = \frac{{7\sqrt 3 }}{6}a\)
\(S = GM'.\frac{{MN + A'C'}}{2} = \frac{{7\sqrt 3 }}{6}a.\frac{{\frac{2}{3}a + a}}{2} = \frac{{35\sqrt 3 }}{{36}}{a^2}\)
Cho đường thẳng a và mặt phẳng \(\left( \alpha \right)\) song song với nhau. Trên a lấy hai điểm tuỳ ý A, B. Gọi A’, B’ lần lượt là các hình chiếu của A, B trên mặt phẳng \(\left( \alpha \right)\) (Hình 8,56).
a) Hỏi ABB'A' là hình gì? Vì sao?
b) Hãy xác định các khoảng cách d(A, \(\left( \alpha \right)\)) và d(B, \(\left( \alpha \right)\)). So sánh các khoảng cách đó.

Phương pháp giải:
Hình bình hành là tứ giác có 2 cặp cạnh đối song song với nhau
Lời giải chi tiết:
a) AA’ và BB’ cùng vuông góc với a nên AA’ // BB’
a song song với \(\left( \alpha \right)\) nên AB // A’B’
Suy ra ABB’A’ là hình bình hành
b) ABB’A’ là hình bình hành nên AA’ = BB’
Vậy d(A, \(\left( \alpha \right)\)) = d(B, \(\left( \alpha \right)\))
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của hình lăng trụ tạo với đáy một góc 600 và hình chiếu vuông góc của đỉnh A’ trên mặt phẳng (ABC) là trung điểm của BC. Tính d(B’C’, (ABC)).
Phương pháp giải:
Khoảng cách giữa d và (P) song song với d là khoảng cách từ một điểm A bất kì thuộc d đến (P).
Lời giải chi tiết:

Gọi D là trung điểm của BC
A’D vuông góc với (ABC)
Suy ra góc A’AD bằng 600
\(A'D = AA'.\sin {60^0} = \frac{{\sqrt 3 }}{2}a\,\)
Vì B’C’ // BC nên B’C’ // (ABC)
Suy ra \(d\left( {B'C',\left( {ABC} \right)} \right) = d\left( {\left( {A'B'C'} \right),\left( {ABC} \right)} \right) = A'D = \frac{{\sqrt 3 }}{2}a\)
Xét hình hộp ABCD.A’B’C’D’. Gọi M, N là 2 điểm bất kì thuộc đáy (A'B'C'D') và M, N lần lượt là hình chiếu của M, N trên (ABCD). Hải MNN’M’ là hình gì? Vì sao? Có nhận xét gì về d(M, (ABCD)) VÀ d(N,(ABCD))?

Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
MNN’M’ là hình bình hành vì 2 đáy song song.
d(M, (ABCD)) = d(N,(ABCD)).
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AC = 2a, AA’ = \(\sqrt 2 a\), hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm của cạnh AC. Tính khoảng cách giữa hai đáy của hình lăng trụ này.
Phương pháp giải:
Cho hai mặt phẳng (P) và (Q) song song với nhau. Để tính khoảng cách giữa (P) và (Q) ta thực hiện các bước:
+ Bước 1: Chọn một điểm A trên (P) sao cho khoảng cách từ A đến (Q) có thể được xác định dễ nhất.
+ Bước 2: Kết luận: d((P); (Q)) = d(A; (Q)).
Lời giải chi tiết:

Gọi F là trung điểm của AC nên AF = a
(ABC) // (A’B’C) nên \(d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = d\left( {A',\left( {ABC} \right)} \right) = A'F\)
Xét tam giác A’AF vuông tại F có:
\(A'F = \sqrt {AA{'^2} - A{F^2}} = \sqrt {2{a^2} - {a^2}} = a\)
Trong một tiết học bơi, thầy giáo dạy bơi chỉ về phía bục nhảy và hỏi học sinh của mình: "Làm sao để tính được khoảng cách từ mặt sản của bục nhảy đến mặt nước. Trong lúc các học sinh khác đang suy nghĩ thì có một ban đã đưa ra câu trả lời như sau: "Em sẽ cầm một sợi dây thừng dài, leo lên bục nhảy, thả một dầu dạy xuống cho đến khi nào dầu dây chạm mặt nước thì đánh dấu vị trí của dây tại vị trí mặt sàn của bục nhảy. Sau do, thu dây lại và do chiều dài của đoạn dây (từ dầu dãy đến vị trí đã đánh dấu) thì do chính là khoảng cách cần tim - Cách làm của bạn ấy có dùng không? Vì sao?

Phương pháp giải:
Khoảng cách giữa 2 mặt song song là khoảng cách từ 1 điểm bất kì của mặt phẳng này đến mặt phẳng kia.
Lời giải chi tiết:
Cách làm của bạn ấy đúng vì khoảng cách giữa 2 mặt song song là khoảng cách từ 1 điểm bất kì của mặt phẳng này đến mặt phẳng kia.
Mục 2 trong sách giáo khoa Toán 11 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các khái niệm cơ bản, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Việc nắm vững kiến thức trong mục này là vô cùng quan trọng, vì nó là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
Để giúp các em học sinh hiểu rõ hơn về nội dung Mục 2, chúng ta sẽ đi vào phân tích chi tiết từng phần của chương này:
Trang 74 giới thiệu khái niệm đạo hàm của hàm số tại một điểm. Đạo hàm được định nghĩa là giới hạn của tỷ số giữa độ biến thiên của hàm số và độ biến thiên của đối số khi độ biến thiên của đối số tiến tới 0. Công thức tính đạo hàm tại một điểm là:
f'(x0) = limΔx→0 (f(x0 + Δx) - f(x0)) / Δx
Các em cần nắm vững định nghĩa này để hiểu rõ bản chất của đạo hàm và cách tính đạo hàm của các hàm số đơn giản.
Trang 75 trình bày các quy tắc tính đạo hàm cơ bản, bao gồm:
Việc thành thạo các quy tắc này sẽ giúp các em tính đạo hàm của các hàm số phức tạp một cách nhanh chóng và chính xác.
Trang 76 và 77 chứa các bài tập vận dụng để giúp các em củng cố kiến thức đã học. Các bài tập này bao gồm việc tính đạo hàm của các hàm số khác nhau, tìm đạo hàm của hàm số tại một điểm, và giải các bài toán liên quan đến đạo hàm.
Dưới đây là lời giải chi tiết cho một số bài tập tiêu biểu trong Mục 2:
Lời giải:
f'(x) = (x3)' + 2(x2)' - 5(x)' + (1)' = 3x2 + 4x - 5 + 0 = 3x2 + 4x - 5
Lời giải:
g'(x) = [(x2 + 1)'(x - 1) - (x2 + 1)(x - 1)'] / (x - 1)2 = [2x(x - 1) - (x2 + 1)] / (x - 1)2 = (2x2 - 2x - x2 - 1) / (x - 1)2 = (x2 - 2x - 1) / (x - 1)2
Để học tốt môn Toán 11, các em nên:
Hy vọng rằng với những kiến thức và lời giải chi tiết trên, các em học sinh sẽ hiểu rõ hơn về Mục 2 trang 74, 75, 76, 77 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!