Chào mừng bạn đến với bài học lý thuyết Hàm số mũ và hàm số logarit, một phần quan trọng trong chương trình SGK Toán 11. Tại giaitoan.edu.vn, chúng tôi cung cấp kiến thức nền tảng vững chắc, giúp bạn dễ dàng tiếp cận và giải quyết các bài toán liên quan.
Bài học này sẽ trình bày chi tiết các khái niệm, tính chất, và ứng dụng của hàm số mũ và hàm số logarit, đồng thời cung cấp các ví dụ minh họa cụ thể để bạn hiểu rõ hơn.
A. Lý thuyết 1. Hàm số mũ a) Định nghĩa
A. Lý thuyết
1. Hàm số mũ
a) Định nghĩa
| Cho a là một số thực dương và khác 1. Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a. |
Lưu ý:
- Hàm số \(y = {a^x}\) \((a > 0,a \ne 1)\) có tập xác định là \(\mathbb{R}\) và tập giá trị là \((0; + \infty )\).
- Hàm số \(y = {a^x}\) liên tục trên \(\mathbb{R}\).
- Với a = 1 thì \({1^x} = 1\) với mọi \(x \in \mathbb{R}\).
b) Đồ thị của hàm số \(y = {a^x}\) \((a > 0,a \ne 1)\)
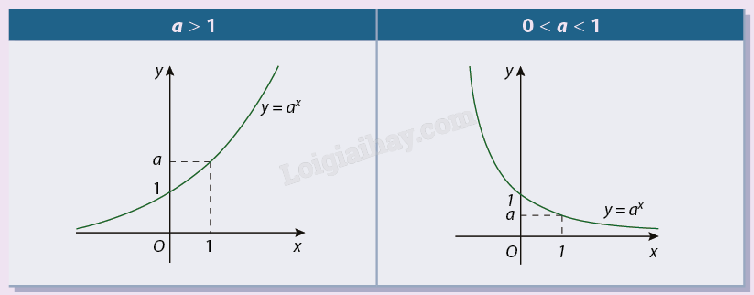
Hàm số mũ \(y = {a^x}\) \((a > 0,a \ne 1)\) có tập xác định là \(\mathbb{R}\) và tập giá trị là \((0; + \infty )\). Hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) khi a > 1 và nghịch biến trên \(\mathbb{R}\) khi 0 < a < 1. Với a > 1 thì \(\mathop {\lim }\limits_{x \to - \infty } {a^x} = 0\); \(\mathop {\lim }\limits_{x \to + \infty } {a^x} = + \infty \). Với 0 < a < 1 thì \(\mathop {\lim }\limits_{x \to - \infty } {a^x} = + \infty \); \(\mathop {\lim }\limits_{x \to + \infty } {a^x} = 0\). Đồ thị (C) của hàm số \(y = {a^x}\) luôn nằm phía trên trục hoành, luôn đi qua các điểm (0;1) và (1;a). |
2. Hàm số logarit
a) Định nghĩa
| Cho số thực dương a khác 1. Hàm số \(y = {\log _a}x\) được gọi là hàm số logarit cơ số a. |
Lưu ý:
- Hàm số \(y = {\log _a}x\) có tập xác định là \(D = (0; + \infty )\) và tập giá trị là \(\mathbb{R}\).
- Hàm số \(y = {\log _a}x\) liên tục trên khoảng \(D = (0; + \infty )\).
- Hàm số \(y = {\log _a}(u(x))\) \((a > 0,a \ne 1)\) xác định khi và chỉ khi u(x) xác định và u(x) > 0.
b) Đồ thị của hàm số logarit \(y = {\log _a}(u(x))\) \((a > 0,a \ne 1)\)
Hàm số logarit \(y = {\log _a}x\) \((a > 0,a \ne 1)\) có tập xác định là \((0; + \infty )\) và tập giá trị là \(\mathbb{R}\). Hàm số \(y = {\log _a}x\) đồng biến trên \((0; + \infty )\) khi a > 1 và nghịch biến trên \((0; + \infty )\) khi 0 < a < 1. Với a > 1 thì \(\mathop {\lim }\limits_{x \to {0^ + }} ({\log _a}x) = - \infty \); \(\mathop {\lim }\limits_{x \to + \infty } ({\log _a}x) = + \infty \). Với 0 < a < 1 thì \(\mathop {\lim }\limits_{x \to {0^ + }} ({\log _a}x) = + \infty \); \(\mathop {\lim }\limits_{x \to + \infty } ({\log _a}x) = - \infty \). Đồ thị (C) của hàm số \(y = {\log _a}x\) luôn nằm phía bên phải trục tung, luôn đi qua các điểm (1;0) và (a;1). |

B. Bài tập
Bài 1: Hàm số nào sau đây là hàm số mũ? Tìm cơ số của hàm số mũ đó.
a) \(y = {2^x}\).
b) \(y = {(\sqrt 2 - 1)^x}\).
c) \(y = {e^x}\).
d) \(y = {x^e}\).
Giải:
a) Hàm số \(y = {2^x}\) là hàm số mũ với cơ số bằng 2.
b) Hàm số \(y = {(\sqrt 2 - 1)^x}\) là hàm số mũ với cơ số bằng \(\sqrt 2 - 1\).
c) Hàm số \(y = {e^x}\) là hàm số mũ với cơ số bằng e.
d) Hàm số \(y = {x^e}\) không phải là hàm số mũ vì cơ số không phải hằng số.
Bài 2: Tìm hàm số mũ \(f(x) = {a^x}\) mà dồ thị của nó được cho bên dưới:
a)
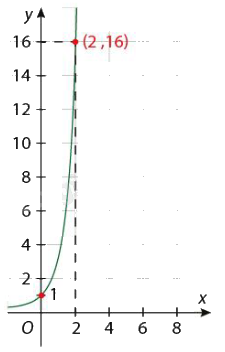
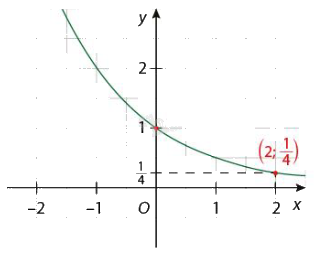
b)
Giải:
a) Vì \(f(x) = {a^2} = 16\) nên a = 4. Do đó \(f(x) = {4^x}\).
b) Vì \(f(x) = {a^2} = \frac{1}{4}\) nên \(a = \frac{1}{2}\). Do đó \(f(x) = {\left( {\frac{1}{2}} \right)^x}\).
Bài 3: Xác định cơ số của các hàm số logarit sau:
a) \(y = {\log _3}x\).
b) \(y = \ln x\).
c) \(y = \log x\).
Giải:
a) Hàm số \(y = {\log _3}x\) có cơ số bằng 3.
b) Hàm số \(y = \ln x\) có cơ số bằng e.
c) Hàm số \(y = \log x\) có cơ số bằng 10.
Bài 4: Tìm hàm số logarit \(f(x) = {\log _a}x\) mà đồ thị của nó được cho bên dưới:
a)
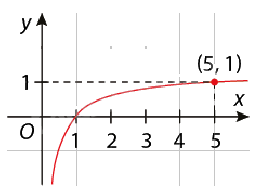
b)
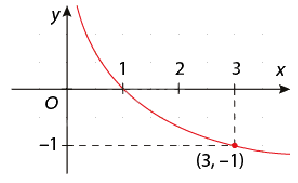
Giải:
a) Vì f(5) = 1 nên \({\log _a}5 = 1 \Leftrightarrow a = 5\). Do đó \(f(x) = {\log _5}x\).
b) Vì f(3) = -1 nên \({\log _a}3 = - 1 \Leftrightarrow a = \frac{1}{3}\). Do đó \(f(x) = {\log _{\frac{1}{3}}}x\).
Hàm số mũ và hàm số logarit là hai loại hàm số quan trọng trong toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực như tài chính, khoa học tự nhiên, và kỹ thuật. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan đến hai loại hàm số này là rất cần thiết cho học sinh lớp 11.
1. Định nghĩa: Hàm số mũ là hàm số có dạng y = ax, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1). x là biến số.
2. Tập xác định: Tập xác định của hàm số mũ y = ax là tập số thực ℝ.
3. Tính chất:
4. Đồ thị: Đồ thị của hàm số mũ y = ax có các đặc điểm sau:
1. Định nghĩa: Hàm số logarit là hàm số có dạng y = logax, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1). x là biến số.
2. Tập xác định: Tập xác định của hàm số logarit y = logax là tập hợp các số thực dương (x > 0).
3. Tính chất:
4. Đồ thị: Đồ thị của hàm số logarit y = logax có các đặc điểm sau:
Hàm số mũ và hàm số logarit là hai hàm số nghịch đảo của nhau. Điều này có nghĩa là:
1. Xác định tập xác định của hàm số: Yêu cầu học sinh xác định điều kiện để hàm số có nghĩa.
2. Tìm giá trị của x: Giải phương trình mũ hoặc phương trình logarit để tìm giá trị của x.
3. So sánh các giá trị: Sử dụng tính chất đơn điệu của hàm số mũ và hàm số logarit để so sánh các giá trị.
4. Biến đổi biểu thức: Sử dụng các công thức logarit để biến đổi biểu thức về dạng đơn giản hơn.
Ví dụ 1: Giải phương trình 2x = 8
Giải: Ta có 2x = 23, suy ra x = 3.
Ví dụ 2: Tính log39
Giải: Ta có log39 = log332 = 2.
Lý thuyết Hàm số mũ và hàm số logarit là một phần quan trọng của chương trình Toán 11. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin hơn. Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để hiểu sâu hơn về hai loại hàm số này.