Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng ta sẽ cùng nhau khám phá và giải quyết các bài tập trong mục 3 trang 83 SGK Toán 11 tập 2. Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức và tự tin hơn trong việc giải toán.
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ cạnh bên bằng 8a
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ cạnh bên bằng 8a, cạnh đáy lớn bằng 5a, cạnh đáy nhỏ bằng a. Tính thể tích hình chóp cụt đều này.
Phương pháp giải:
Áp dụng công thức tính thể tích khối chóp cụt đều có chiều cao h và diện tích 2 đáy lần lượt là S và S’: \(V = \frac{1}{3}h\left( {S + S' + \sqrt {SS'} } \right)\)
Lời giải chi tiết:
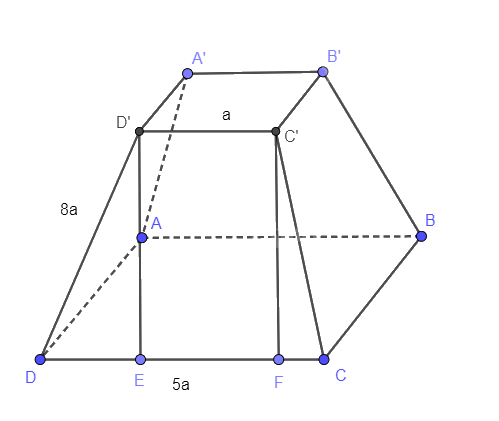
Kẻ D’E và D’F vuông góc với CD nên D’E // D’F
Mà C’D’ // EF nên D’C’FE là hình bình hành. Suy ra EF = D’C’ = a
\( \Rightarrow DE + CF = DC - EF = 5a - a = 4a\)\( \Rightarrow DE = CF = 2a\)
\(D'E = \sqrt {D'{B^2} - D{E^2}} = \sqrt {{{\left( {8a} \right)}^2} - {{\left( {2a} \right)}^2}} = 2\sqrt {15} a\)
\({S_{ABCD}} = {\left( {5a} \right)^2} = 25{a^2}\)
\({S_{A'B'C'D'}} = {a^2}\)
\( \Rightarrow V = \frac{1}{3}.2\sqrt {15} a.\left( {25{a^2} + {a^2} + \sqrt {25{a^2}.{a^2}} } \right) = \frac{{62\sqrt {15} }}{3}{a^3}\)
Bạn An muốn làm các viên nước đá có dạng khối chóp cụt tứ giác đều có đáy lớn bằng 3 cm, đáy nhỏ bằng 1,5 cm và cao 3 cm bằng cách dùng khay đá, mỗi khay sẽ tạo được 6 viên đá. Hỏi bạn An cần ít nhất bao nhiêu khay để chứa đồng thời 2 lít nước?
Phương pháp giải:
Áp dụng công thức tính thể tích khối chóp cụt đều có chiều cao h và diện tích 2 đáy lần lượt là S và S’: \(V = \frac{1}{3}h\left( {S + S' + \sqrt {SS'} } \right)\) để tính thể tích mỗi viên nước đá.
Lời giải chi tiết:
2 lít = 2000 cm3
\(V = \frac{1}{3}.3.\left( {{3^2} + 1,{5^2} + \sqrt {{3^2}.1,{5^2}} } \right) = 15,75\) (cm3)
Từ 2 lít nước có thể tạo ra số viên đá là: \(2000:15,75 \approx 127\) (viên)
Ta có: \(\frac{{127}}{6} \approx 21,2\)
Vậy cần ít nhất 22 khay nước để chứa đồng thời 2 lít nước.
Mục 3 trang 83 SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, trước hết, chúng ta cần nắm vững lý thuyết liên quan. Hãy cùng nhau ôn lại các khái niệm, định lý và công thức quan trọng trước khi bắt đầu giải bài tập.
Bài tập 1 thường là bài tập áp dụng trực tiếp kiến thức lý thuyết. Để giải bài tập này, bạn cần:
Ví dụ, nếu bài tập yêu cầu tính đạo hàm của một hàm số, bạn cần áp dụng các quy tắc tính đạo hàm đã học để tìm ra kết quả chính xác.
Bài tập 2 có thể là bài tập nâng cao hơn, đòi hỏi bạn phải vận dụng kiến thức một cách linh hoạt và sáng tạo. Để giải bài tập này, bạn cần:
Ví dụ, nếu bài tập yêu cầu chứng minh một đẳng thức, bạn cần sử dụng các phép biến đổi đại số để đưa đẳng thức về dạng đơn giản và chứng minh nó.
Bài tập 3 có thể là bài tập thực tế, liên hệ với các ứng dụng của toán học trong đời sống. Để giải bài tập này, bạn cần:
Ví dụ, nếu bài tập yêu cầu tính diện tích của một mảnh đất, bạn cần sử dụng các công thức tính diện tích hình học để tìm ra kết quả chính xác.
Để đạt được kết quả tốt nhất khi giải bài tập mục 3 trang 83 SGK Toán 11 tập 2, bạn cần:
Kiến thức trong mục 3 trang 83 SGK Toán 11 tập 2 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả hơn.
Hy vọng rằng, với những hướng dẫn chi tiết và dễ hiểu trên đây, bạn đã có thể tự tin giải quyết các bài tập trong mục 3 trang 83 SGK Toán 11 tập 2. Chúc bạn học tập tốt và đạt được kết quả cao trong môn Toán!