Bài 4.13 trang 105 SGK Toán 11 tập 1

Bài 4.13 trang 105 SGK Toán 11 tập 1 - Cùng khám phá

Bài 4.13 trang 105 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.

Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho bài 4.13 trang 105 SGK Toán 11 tập 1, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.

Cho tứ diện ABCD. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC, ACD. Chứng minh rằng đường thẳng GG’ song song với hai mặt phẳng (ABD) và (BCD).

Đề bài

Cho tứ diện ABCD. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC, ACD. Chứng minh rằng đường thẳng GG’ song song với hai mặt phẳng (ABD) và (BCD).

Phương pháp giải - Xem chi tiết Bài 4.13 trang 105 SGK Toán 11 tập 1 - Cùng khám phá 1

Chứng minh đường thẳng a không thuộc (P) song song với mặt phẳng (P):

+ Tìm đường thẳng b thuộc (P) sao cho a // b.

+ Suy ra a // (P).

Lời giải chi tiết

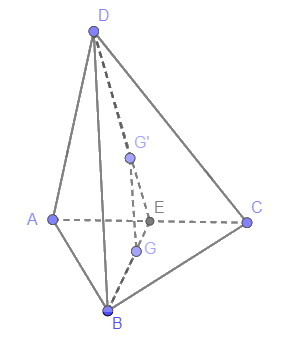
Bài 4.13 trang 105 SGK Toán 11 tập 1 - Cùng khám phá 2

Gọi E là trung điểm AC

\( \Rightarrow EG = \frac{1}{3}BE,EG' = \frac{1}{3}DE\)

Xét tam giác EDB có \(\frac{{EG}}{{BE}} = \frac{{EG'}}{{DE}} = \frac{1}{3}\) nên GG’ // BD

Suy ra GG’ // (BCD), GG’ // (BCD).

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 4.13 trang 105 SGK Toán 11 tập 1 - Cùng khám phá – hành trang không thể thiếu trong chuyên mục Sách giáo khoa Toán 11 trên nền tảng đề thi toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 4.13 trang 105 SGK Toán 11 tập 1 - Giải chi tiết

Bài 4.13 trang 105 SGK Toán 11 tập 1 thuộc chương trình Đại số, cụ thể là phần Đạo hàm. Bài toán này thường yêu cầu học sinh áp dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác.

Nội dung bài toán

Thông thường, bài 4.13 sẽ đưa ra một hàm số cụ thể và yêu cầu tính đạo hàm của hàm số đó tại một điểm cho trước hoặc tìm điều kiện để hàm số có đạo hàm. Đôi khi, bài toán còn yêu cầu sử dụng đạo hàm để giải các bài toán liên quan đến cực trị của hàm số hoặc các bài toán ứng dụng thực tế.

Phương pháp giải

Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần tính đạo hàm.
Chọn quy tắc đạo hàm phù hợp: Dựa vào cấu trúc của hàm số, chọn quy tắc đạo hàm phù hợp (quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp, hàm lượng giác, hàm mũ, hàm logarit,...).
Tính đạo hàm: Áp dụng quy tắc đạo hàm đã chọn để tính đạo hàm của hàm số.
Thay giá trị (nếu cần): Nếu bài toán yêu cầu tính đạo hàm tại một điểm cụ thể, hãy thay giá trị của điểm đó vào đạo hàm vừa tính được.
Kiểm tra lại kết quả: Kiểm tra lại các bước tính toán để đảm bảo kết quả chính xác.

Ví dụ minh họa

Giả sử bài toán yêu cầu tính đạo hàm của hàm số f(x) = sin(2x) tại điểm x = π/4.

Bước 1: Xác định hàm số: f(x) = sin(2x)
Bước 2: Chọn quy tắc đạo hàm: Sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x). Ở đây, u(t) = sin(t) và v(x) = 2x.
Bước 3: Tính đạo hàm: f'(x) = cos(2x) * 2 = 2cos(2x)
Bước 4: Thay giá trị: f'(π/4) = 2cos(2 * π/4) = 2cos(π/2) = 0
Bước 5: Kiểm tra lại kết quả: Kết quả đạo hàm của hàm số tại điểm x = π/4 là 0.

Các dạng bài tập thường gặp

Tính đạo hàm của hàm số đơn giản: Các hàm số đa thức, hàm số lượng giác cơ bản.
Tính đạo hàm của hàm số phức tạp: Hàm số hợp, hàm số ẩn.
Tìm đạo hàm cấp hai: Tính đạo hàm của đạo hàm.
Ứng dụng đạo hàm để giải các bài toán liên quan đến cực trị: Tìm điểm cực đại, cực tiểu của hàm số.
Ứng dụng đạo hàm để giải các bài toán thực tế: Tính vận tốc, gia tốc, tốc độ thay đổi,...