Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 tại giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 2 của chương trình Toán 11 tập 1 thường xoay quanh các chủ đề quan trọng như dãy số, cấp số cộng, cấp số nhân. Việc hiểu rõ và vận dụng thành thạo các kiến thức này là nền tảng cho các chương trình học toán ở các lớp trên.
a) Trên một đường tròn, cung nửa đường tròn có số đo bằng bao nhiêu radian? Góc ở tâm chắn cung nửa đường tròn có số đo bằng bao nhiêu radian? b) Từ đó tìm mối liên hệ giữa đơn vị độ và đơn vị radian.
a) Trên một đường tròn, cung nửa đường tròn có số đo bằng bao nhiêu radian? Góc ở tâm chắn cung nửa đường tròn có số đo bằng bao nhiêu radian?
b) Từ đó tìm mối liên hệ giữa đơn vị độ và đơn vị radian.
Phương pháp giải:
- Theo lý thuyết, cung có độ dài bằng r (bán kính) là cung có số đo 1 rad.
\( \Rightarrow \) Cung có độ dài \(l\) thì có số đo là \(\frac{l}{r}\) rad.
- Cung nửa đường tròn có độ dài là \(\pi r\).
- Theo lý thuyết, góc ở tâm chắn cung có số đo 1 rad là góc có số đo 1 rad.
\( \Rightarrow \)Góc ở tâm chắn cung có số đo \(\alpha \) rad là góc có số đo \(\alpha \) rad.
Lời giải chi tiết:
a) Nửa đường tròn có độ dài là \(\pi r\)\( \Rightarrow \) Cung nửa đường tròn có số đo là \(\frac{{\pi r}}{r} = \pi \) rad.
Do đó góc ở tâm chắn nửa đường tròn có số đo là \(\pi \) rad.
b) Nửa đường tròn có số đo là \(\pi \) rad
Mà số đo nửa đường tròn còn bằng 1800
\( \Rightarrow \)\({180^0} = \pi \) rad
\( \Rightarrow {1^0} = \frac{\pi }{{180}}\) rad; 1 rad \( = {\left( {\frac{{180}}{\pi }} \right)^0}\).
Đổi 5 rad và \(\frac{\pi }{8}\) rad ra độ.
Phương pháp giải:
Áp dụng công thức: \(\alpha \)rad = \({\left( {\alpha .\frac{{180}}{\pi }} \right)^0}\)
Lời giải chi tiết:
5 rad = \({\left( {5.\frac{{180}}{\pi }} \right)^0} = {\left( {\frac{{900}}{\pi }} \right)^0}\)
\(\frac{\pi }{8}\) rad = \({\left( {\frac{\pi }{8}.\frac{{180}}{\pi }} \right)^0} = 22,{5^0}\)
Trên đường tròn bán kính r, hãy tính:
a) Độ dài của cung nửa đường tròn;
b) Độ dài của cung có số đo \(\alpha \) rad.
Phương pháp giải:
Công thức tính độ dài cung là: \(l = \frac{{\pi Rn}}{{180}}\), trong đó \({n^0}\) là số đo cung cần tìm.
Áp dụng công thức: \(\alpha \)rad = \({\left( {\alpha .\frac{{180}}{\pi }} \right)^0}\)
Lời giải chi tiết:
a) Cung nửa đường tròn có số đo là 1800
Độ dài của cung nửa đường tròn là \(l = \frac{{\pi r180}}{{180}} = \pi r\).
b) \(\alpha \)rad = \({\left( {\alpha .\frac{{180}}{\pi }} \right)^0}\)
\(l = \frac{{\pi r}}{{180}}.\frac{{180\alpha }}{\pi } = \alpha r\).
Một bức tường của một ngôi nhà có dạng như Hình 1.7, trong đó cung AB là một cung của đường tròn tâm C, bán kính AC. Tính chu vi của bức tường.
Phương pháp giải:
- Chu vi bức tường gồm phần độ dài cung , AH, BK và HK.
- Áp dụng công thức: Trên đường tròn có bán kính \(r\), cung có số đo \(\alpha \) rad có độ dài \(l = \alpha r\).
- Định lý Py – ta – go cho tam giác vuông: Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết:
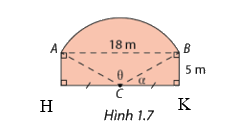
Gọi điểm H, K như trên hình
AB = 18m \( \Rightarrow \)HK = 18m \( \Rightarrow \)CK = 9m
\(\Rightarrow BC = \sqrt {B{K^2} + C{K^2}} = \sqrt {{5^2} + {9^2}} = \sqrt {106} \Rightarrow r = \sqrt {106} \) (m)
Ta có: \(\tan \alpha = \frac{{BK}}{{CK}} = \frac{5}{9}\) \( \Rightarrow \alpha \approx 0,507 rad\)
\(\theta = \pi - 2\alpha = \pi - 2.0,507 \approx 2,128 rad\)
\( \Rightarrow \) Cung AB có độ dài là: \(l = \theta r = 2,128.\sqrt {106} \approx 21,91\)(m)
Vậy chu vi bức tường là: 21,91+5+5+18=49,91 (m)
Hãy xác định số đo của mỗi cung lượng giác (A đến B) khi điểm M di động trên đường tròn từ A đến B trong Hình 1.1.

Phương pháp giải:
- Khi điểm M di động trên đường tròn theo chiều dương từ A đến B tạo nên cung \(\frac{1}{4}\) đường tròn nên có số đo là \(\frac{\pi }{2}\). M đi tiếp mỗi vòng thì thêm \(2\pi \).
- Khi điểm M di động trên đường tròn theo chiều âm từ A đến B tạo nên cung \(\frac{3}{4}\) đường tròn nên có số đo là \( - \frac{{3\pi }}{2}\).
Lời giải chi tiết:
a) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2}\).
b) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2} + 2\pi = \frac{{5\pi }}{2}\).
c) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2} + 2.2\pi = \frac{{9\pi }}{2}\).
d) Cung lượng giác AB (A đến B) có số đo là \( - \frac{{3\pi }}{2}\).
Tính số đo của mỗi góc lượng giác (OA, OB) trong Hình 1.1.

Phương pháp giải:
Theo lý thuyết, số đo của góc lượng giác (OA, OB)là số đo cung lượng giác (A đến B). Kí hiệu: sđ(OA, OB).
Lời giải chi tiết:
a) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2}\). Vậy sđ(OA, OB) =\(\frac{\pi }{2}\).
b) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2} + 2\pi = \frac{{5\pi }}{2}\). Vậy sđ(OA,OB) = \(\frac{{5\pi }}{2}\).
c) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2} + 2.2\pi = \frac{{9\pi }}{2}\). Vậy sđ(OA,OB) = \(\frac{{9\pi }}{2}\).
d) Cung lượng giác AB (A đến B) có số đo là \( - \frac{{3\pi }}{2}\). Vậy sđ(OA,OB) = \( - \frac{{3\pi }}{2}\).
Giả sử sđ(OA, OB) = \(\frac{\pi }{3}\) và sđ(OB, OC) = \(\frac{\pi }{4}\)(Hình 1.11). Xác định sđ(OA, OC).

Phương pháp giải:
Áp dụng hệ thức Chasles: sđ(OA, OB) + sđ(OB, OC) = sđ(OA, OC) + \(k2\pi \), \(k \in \mathbb{Z}\).
Lời giải chi tiết:
Áp dụng hệ thức Chasles: sđ(OA, OB) + sđ(OB, OC) = sđ(OA, OC) + \(k2\pi \), \(k \in \mathbb{Z}\)
\( \Leftrightarrow \frac{\pi }{4} + \frac{\pi }{3} = \frac{{7\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\).
Nếu góc lượng giác (OA, OB) và (OA, OC) lần lượt có số đo là \( - \frac{{7\pi }}{4}\) và \(\frac{{13\pi }}{4}\) thì góc lượng giác (OB, OC) có số đo bằng bao nhiêu, biết rằng \(4\pi < \left( {OB,OC} \right) < 6\pi \)?
Phương pháp giải:
Áp dụng hệ quả của hệ thức Chasles: sđ(OB, OC) = sđ(OA, OC) - sđ(OA, OB) + \(k2\pi \), \(k \in \mathbb{Z}\).
Lời giải chi tiết:
Áp dụng công thức: sđ(OB, OC) = sđ(OA, OC) - sđ(OA, OB) + \(k2\pi \), \(k \in \mathbb{Z}\)
\( \Leftrightarrow - \frac{{7\pi }}{4} - \frac{{13\pi }}{4} + k2\pi = - 5\pi + k2\pi ,k \in \mathbb{Z}\)
Mà \(4\pi < \left( {OB,OC} \right) < 6\pi \)
\(\begin{array}{l} \Rightarrow 4\pi < - 5\pi + k2\pi < 6\pi \\ \Leftrightarrow 9\pi < k2\pi < 11\pi \\ \Leftrightarrow 4,5 < k < 5,5\\ \Rightarrow k = 5\end{array}\)
Vậy sđ(OB, OC) = \( - 5\pi + 5.2\pi = 5\pi \)
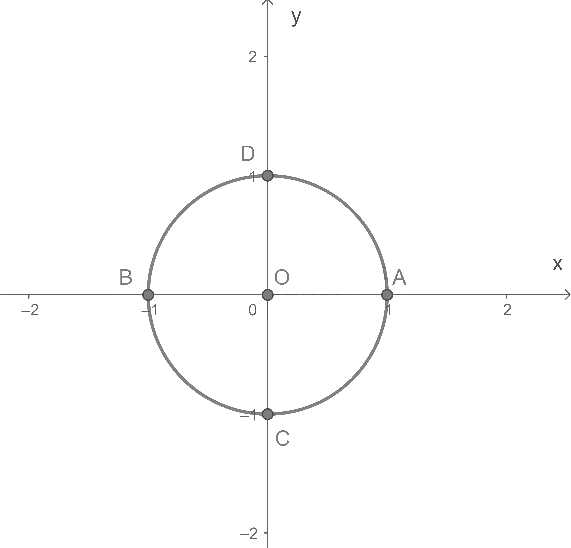
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính R = 1 và tìm giao điểm của nó với các trục tọa độ.
Phương pháp giải:
Vẽ hình và quan sát
Lời giải chi tiết:

Đường tròn tâm O cắt trục Ox tại điểm A(1;0) và B(-1;0), cắt Oy tại điểm C(0;-1) và D(0;1).
Trên đường tròn lượng giác, tìm điểm biểu diễn của các góc lượng giác có số đo sau:
a) \(\frac{{19\pi }}{3}\)
b) \( - {1125^0}\)
Phương pháp giải:
- Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
- Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\alpha \) là điểm M trên đường tròn lượng giác sao cho sđ(OA, OM) = \(\alpha \).
Lời giải chi tiết:
a) \(\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi \)
Vậy điểm biểu diễn góc lượng giác có số đo \(\frac{{19\pi }}{3}\) là điểm C(0;-1).
b) \( - {1125^0} = - {45^0} - {3.360^0}\)
Vậy điểm biểu diễn của góc lượng giác có số đo \( - {1125^0}\) là điểm chính giữa B của cung nhỏ .
Mục 2 trong SGK Toán 11 tập 1 tập trung vào các kiến thức cơ bản về dãy số, cấp số cộng và cấp số nhân. Việc nắm vững các định nghĩa, công thức và phương pháp giải bài tập liên quan đến các chủ đề này là vô cùng quan trọng. Bài viết này sẽ cung cấp một cái nhìn tổng quan về mục 2, đồng thời hướng dẫn chi tiết cách giải các bài tập từ trang 3 đến trang 7.
Dãy số là một tập hợp hữu hạn hoặc vô hạn các số được sắp xếp theo một thứ tự nhất định. Mỗi số trong dãy số được gọi là một phần tử của dãy số. Để hiểu rõ hơn về dãy số, chúng ta cần nắm vững các khái niệm sau:
Cấp số cộng là một dãy số mà mỗi số hạng sau đều lớn hơn (hoặc nhỏ hơn) số hạng trước một lượng không đổi, gọi là công sai (d). Các công thức quan trọng liên quan đến cấp số cộng bao gồm:
Cấp số nhân là một dãy số mà mỗi số hạng sau đều bằng số hạng trước nhân với một lượng không đổi, gọi là công bội (q). Các công thức quan trọng liên quan đến cấp số nhân bao gồm:
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu từ trang 3 đến trang 7 SGK Toán 11 tập 1:
Cho dãy số (un) với un = 2n + 1. Tìm số hạng thứ 5 và số hạng thứ 10 của dãy số.
Giải:
u5 = 2 * 5 + 1 = 11
u10 = 2 * 10 + 1 = 21
Cho cấp số cộng có số hạng đầu u1 = 3 và công sai d = 2. Tìm số hạng thứ 7 và tổng của 7 số hạng đầu tiên.
Giải:
u7 = u1 + (7-1)d = 3 + 6 * 2 = 15
S7 = 7/2 * (u1 + u7) = 7/2 * (3 + 15) = 63
Cho cấp số nhân có số hạng đầu u1 = 2 và công bội q = 3. Tìm số hạng thứ 6 và tổng của 6 số hạng đầu tiên.
Giải:
u6 = u1 * q(6-1) = 2 * 35 = 486
S6 = u1 * (1 - q6) / (1 - q) = 2 * (1 - 36) / (1 - 3) = 728
Để giải bài tập về dãy số, cấp số cộng và cấp số nhân một cách hiệu quả, các em cần lưu ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập khác trong SGK và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài giảng online hoặc tham gia các khóa học luyện thi để được hướng dẫn chi tiết hơn.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích và phương pháp giải bài tập hiệu quả cho mục 2 trang 3, 4, 5, 6, 7 SGK Toán 11 tập 1. Chúc các em học tập tốt!