Bài 8.16 trang 72 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải nhanh chóng và hiệu quả, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai mặt phẳng (SAB) và (SAC)
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai mặt phẳng (SAB) và (SAC) củng vuông góc với mặt đáy. Chứng minh: \(\left( {SCD} \right) \bot \left( {SAD} \right),\left( {SBC} \right) \bot \left( {SAB} \right),\left( {SBD} \right) \bot \left( {SAC} \right)\).
Phương pháp giải - Xem chi tiết
Hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến vuông góc với mặt phẳng thứ ba.
Mặt phẳng (P) chứa 2 đường thẳng cắt nhau cùng vuông góc với d thì (P) vuông góc với d.
Nếu trên mặt phẳng này có chứa 1 đường thẳng vuông góc với mặt phẳng kia thì 2 mặt phẳng đó vuông góc với nhau.
Lời giải chi tiết
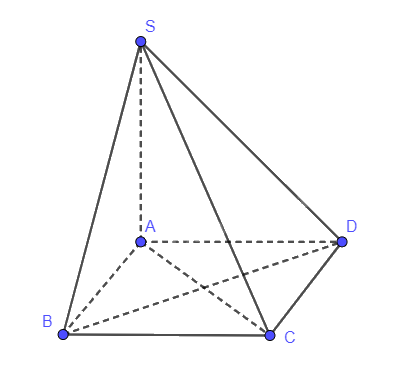
(SAB) và (SAC) củng vuông góc với (ABCD) nên SA vuông góc với (ABCD)
Suy ra SA vuông góc với CD, BC, BD
Mà AD vuông góc với CD
Nên CD vuông góc với (SAD)
Suy ra \(\left( {SCD} \right) \bot \left( {SAD} \right)\)
SA vuông góc với BC và AB vuông góc với BC nên BC vuông góc với (SAB)
Suy ra (SBC) vuông góc với (SAB)
SA vuông góc với BD và AC vuông góc với BD nên (SAC) vuông góc với BD
Suy ra (SAC) vuông góc với (SBD)
Bài 8.16 SGK Toán 11 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến việc tối ưu hóa một đại lượng nào đó bằng cách sử dụng đạo hàm. Để giải bài toán này, học sinh cần nắm vững các kiến thức về:
Nội dung bài toán:
Thông thường, bài 8.16 sẽ đưa ra một tình huống thực tế, ví dụ như việc thiết kế một hình hộp chữ nhật có thể tích cho trước và yêu cầu tìm kích thước của hình hộp để diện tích bề mặt nhỏ nhất. Hoặc bài toán về việc tìm kích thước của một mảnh đất hình chữ nhật có chu vi cho trước để diện tích lớn nhất.
Phương pháp giải:
Ví dụ minh họa:
Giả sử chúng ta có bài toán sau:
Một người nông dân có 100m hàng rào để rào một mảnh đất hình chữ nhật. Hỏi mảnh đất đó có kích thước như thế nào để có diện tích lớn nhất?
Giải:
Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là x và y (x, y > 0). Chu vi của mảnh đất là 2(x + y) = 100, suy ra x + y = 50, hay y = 50 - x.
Diện tích của mảnh đất là S = xy = x(50 - x) = 50x - x2.
Đạo hàm của S theo x là S' = 50 - 2x.
Giải phương trình S' = 0, ta được x = 25.
Đạo hàm bậc hai của S là S'' = -2 < 0, suy ra x = 25 là điểm cực đại của hàm số S.
Khi x = 25, y = 50 - 25 = 25.
Vậy mảnh đất có kích thước 25m x 25m để có diện tích lớn nhất.
Lưu ý:
Tài liệu tham khảo:
Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng này, các bạn học sinh sẽ tự tin hơn khi giải bài 8.16 trang 72 SGK Toán 11 tập 2 và các bài tập tương tự. Chúc các bạn học tốt!