Chào mừng các em học sinh đến với bài giải mục 3 trang 139 SGK Toán 11 tập 1 trên giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Mục 3 trang 139 tập trung vào các bài tập về... (Nội dung cụ thể của mục 3 sẽ được điền vào đây sau khi xác định rõ nội dung). Hãy cùng chúng tôi khám phá và chinh phục những thử thách toán học này!
Bảng 5.12 cho biết về phân phối khối lượng của một nhóm 32 học sinh
Bảng 5.12 cho biết về phân phối khối lượng của một nhóm 32 học sinh
a, Xác định nhóm chứa trung vị \({M_e}\) của mẫu số liệu đã cho. Tính \({M_e}\)
b, Kí hiệu \({u_1},{u_2},...{u_{32}}\) là các giá trị của mẫu số liệu được sắp xếp theo thứ tự không giảm. Nhóm dưới \({M_e}\) có bao nhiêu giá trị? Nhóm trên \({M_e}\) có bao nhiêu giá trị?
c, Hãy giải thích vì sao Bảng 5.20 a và Bảng 5.20 b tương ứng là bảng phân bố tần số của nhóm dưới và bảng phân bố tần số của nhóm trên.
d, Tính các tứ phân vị thứ nhất \({Q_1}\) , (trung vị của nhóm dưới) và tứ phân vị thứ ba \({Q_3}\)( trung vị của nhóm trên) của mẫu số liệu cho trong Bảng 5.20 .
Phương pháp giải:
a, Lập bảng tần số ghép nhóm để xác định nhóm trung vị và công thức tính \({M_e}\)
b, Dựa vào câu a để xác định
c, Do khoảng cách nhóm trung vị là 5 và tần số nhóm là 7 nên chia đều khoảng cách có 5 giá trị nhỏ hơn \({M_e}\) và 2 giá trị lớn hơn bằng \({M_e}\).
d, Dựa vào công thức tính trung vị để xác định \({Q_1}\), \({Q_3}\).
Lời giải chi tiết:
a,

Ta có: \(\frac{N}{2} = \frac{{32}}{2} = 16\). Nhóm trung vị là [40,45).
\({L_m} = 40\), \(\frac{N}{2} = \frac{{32}}{2} = 16\), T= 11,\({n_m} = 7\) , h= 5
\({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 40 + \frac{{16 - 11}}{7}.5 \approx 43,57\)
b, Do \({M_e}\) thuộc nhóm [40,45) nên
Tổng giá trị nhỏ hơn \({M_e}\) là : 5+6=11
Tổng giá trị lớn hơn \({M_e}\) là: 2+5+4+3=14
c, Dựa vào câu c nên Bảng 5.20 a và Bảng 5.20 b tương ứng là bảng phân bố tần số của nhóm dưới và bảng phân bố tần số của nhóm trên.
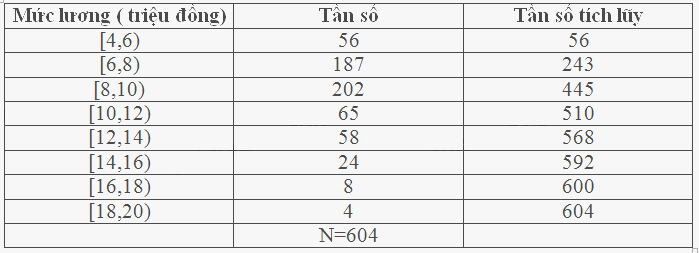
d Tính \({Q_1}\): Bảng tần số tích lũy
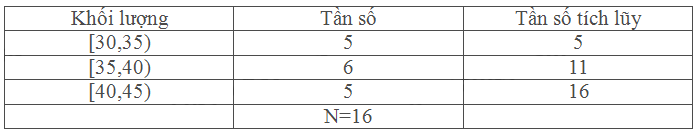
Ta có:\(\frac{N}{2} = \frac{{16}}{2} = 8\). Nhóm trung vị là [35,40).
\({L_1} = 35\), \(\frac{N}{2} = \frac{{16}}{2} = 8\), T= 5,\({n_1} = 6\) , h= 5
\({Q_1} = {M_e} = {L_1} + \frac{{\frac{N}{2} - T}}{{{n_1}}}.h = 35 + \frac{{8 - 5}}{6}.5 = 37,5\)
Tính \({Q_3}\): Bảng tần số tích lũy

Ta có:\(\frac{N}{2} = \frac{{16}}{2} = 8\). Nhóm trung vị là [50,55).
\({L_3} = 50\), \(\frac{N}{2} = \frac{{16}}{2} = 8\), T= 7,\({n_3} = 4\) , h= 5
\({Q_3} = {M_e} = {L_3} + \frac{{\frac{N}{2} - T}}{{{n_3}}}.h = 50 + \frac{{8 - 7}}{4}.5 = 51,25\)
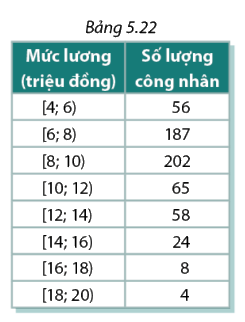
Bảng 5.22 biểu diễn kết quả điều tra do Ban chấp hành Công đoàn của một xí nghiệp may thực hiện về lương hàng tháng của 604 công nhân và cán bộ lãnh đạo
a, Ban chấp hành Công đoàn muốn đề nghị trợ cấp cho nhóm 25% số công nhân có mức lương thấp nhất trong công ty. Hãy ước tính mức lương cao nhất của nhóm công nhân này. ( làm tròn kết quả đến hai chữ số thập phân)
b, Để có thêm thông tin nhằm hoạch định vấn đề lương thưởng cho năm tới, Ban giám đốc căn cứ vào 50% công nhân có lương nằm ở trung tâm của mẫu số liệu. Hãy xác định mức lương thấp nhất và mức lương cao nhất của nhóm công nhân này ( làm tròn kết quả đến hai chữ số thập phân)

Phương pháp giải:
a, Tính \({Q_1}\) để tìm mức lương cao nhất của 25% số công nhân
b, Tính \({Q_2}\) và \({Q_3}\)
Lời giải chi tiết:
a, Bảng tần số tích lũy

Ta có: \(\frac{N}{2} = \frac{{604}}{2} = 302 \Rightarrow \frac{N}{4} = \frac{{604}}{4} = 151 \Rightarrow \frac{{3N}}{4} = 453\)
Các nhóm chứa \({Q_1}\), \({Q_2}\) và \({Q_3}\) là [6,8), [8,10) và [10,12)
Độ dài các nhóm ghép đều bằng 2
Ta có: \({L_1} = 6,{n_1} = 187,{T_1} = 56\)\( \Rightarrow {Q_1} = {L_1} + \frac{{\frac{N}{4} - {T_1}}}{{{n_1}}}.h = 6 + \frac{{151 - 56}}{{187}}.2 \approx 7,02\)( triệu đồng)
Mức lương cao nhất của nhóm công ty này là xấp xỉ 7,02 triệu đồng
b, Ta có: \({L_2} = 8,{n_2} = 202,{T_2} = 243\)\( \Rightarrow {Q_2} = {L_2} + \frac{{\frac{N}{2} - {T_2}}}{{{n_2}}}.h = 8 + \frac{{302 - 243}}{{202}}.2 \approx 8,58\)
\({L_3} = 10,{n_3} = 65,{T_3} = 445\)\( \Rightarrow {Q_3} = {L_3} + \frac{{\frac{{3N}}{4} - {T_3}}}{{{n_3}}}.h = 10 + \frac{{453 - 445}}{{65}}.2 \approx 10,25\)
Vậy mức lương cao nhất và thấp nhất của 50% nhóm công nhân trung tâm là xấp xỉ 10,25 triệu đồng và 8,58 triệu đồng.
Mục 3 trang 139 SGK Toán 11 tập 1 thường xoay quanh các bài tập liên quan đến một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững kiến thức lý thuyết, hiểu rõ các định nghĩa, định lý và công thức liên quan. Bài viết này sẽ cung cấp một hướng dẫn chi tiết về cách tiếp cận và giải quyết các bài tập trong mục 3, đồng thời đưa ra các ví dụ minh họa cụ thể.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải xác định rõ chủ đề mà mục 3 đề cập đến. Ví dụ, nếu mục 3 liên quan đến hàm số bậc hai, học sinh cần ôn lại các kiến thức về:
Sau khi nắm vững kiến thức lý thuyết, học sinh cần đọc kỹ đề bài và phân tích các thông tin đã cho. Xác định rõ yêu cầu của bài toán là gì, các dữ kiện nào là quan trọng và cần sử dụng kiến thức nào để giải quyết. Đôi khi, việc vẽ một hình minh họa có thể giúp học sinh hình dung rõ hơn về bài toán và tìm ra hướng giải phù hợp.
Khi đã xác định được hướng giải, học sinh có thể áp dụng kiến thức lý thuyết và các công thức liên quan để giải bài tập. Lưu ý, cần trình bày các bước giải một cách rõ ràng, logic và có giải thích cụ thể để người đọc có thể hiểu được quá trình suy luận của mình.
Sau khi giải xong bài tập, học sinh nên kiểm tra lại kết quả để đảm bảo tính chính xác. Có thể thay thế các giá trị đã tìm được vào đề bài để kiểm tra xem chúng có thỏa mãn các điều kiện đã cho hay không. Ngoài ra, có thể so sánh kết quả của mình với các lời giải khác để tìm ra những sai sót và sửa chữa kịp thời.
Bài tập: Tìm tập xác định của hàm số y = √(2x - 1) / (x - 3)
Giải:
Để nâng cao kỹ năng giải toán, học sinh cần luyện tập thường xuyên với nhiều dạng bài tập khác nhau. Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo, bạn bè hoặc tìm kiếm sự giúp đỡ trên các diễn đàn, trang web học toán online như giaitoan.edu.vn. Việc trao đổi, thảo luận với người khác có thể giúp học sinh hiểu sâu hơn về bài toán và tìm ra những cách giải mới.
Tùy thuộc vào nội dung cụ thể của chương trình học, mục 3 trang 139 có thể chứa các dạng bài tập khác nhau. Một số dạng bài tập thường gặp bao gồm:
Hiện nay, có rất nhiều công cụ hỗ trợ học tập có thể giúp học sinh giải toán nhanh chóng và hiệu quả hơn. Một số công cụ hữu ích bao gồm:
Tuy nhiên, học sinh không nên quá phụ thuộc vào các công cụ này mà cần rèn luyện kỹ năng giải toán một cách độc lập. Các công cụ chỉ nên được sử dụng như một phương tiện hỗ trợ, giúp kiểm tra lại kết quả hoặc giải quyết các bài toán phức tạp.
Giải mục 3 trang 139 SGK Toán 11 tập 1 đòi hỏi học sinh phải nắm vững kiến thức lý thuyết, rèn luyện kỹ năng giải toán và có phương pháp học tập hiệu quả. Hy vọng rằng, với những hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, các em sẽ tự tin chinh phục những bài tập toán học và đạt kết quả tốt trong học tập.