Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 83, 84 SGK Toán 11 tập 1 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em trong quá trình học tập môn Toán.
Các hàm số \(f\left( x \right) = {x^3} - 3x + 2\) và \(g\left( x \right) = \sin x\) xác định trên \(\left( { - \infty ; + \infty } \right)\) có đồ thị như sau:
Các hàm số \(f\left( x \right) = {x^3} - 3x + 2\) và \(g\left( x \right) = \sin x\) xác định trên \(\left( { - \infty ; + \infty } \right)\) có đồ thị như sau:
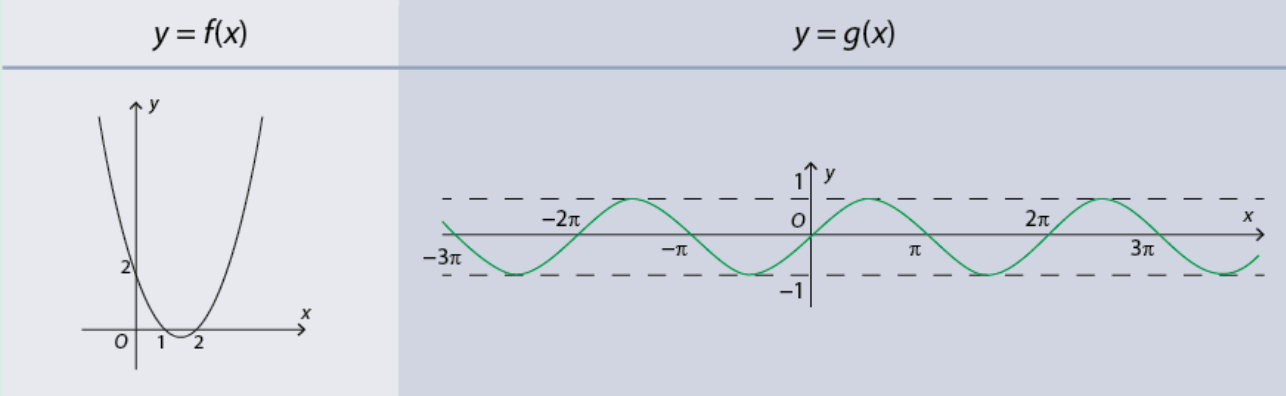
Dựa vào đồ thị, hãy dự đoán tính liên tục của các hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) trên \(\left( { - \infty ; + \infty } \right)\).
Phương pháp giải:
Đồ thị hàm số liên tục trên một khoảng là đường liền trên khoảng đó
Lời giải chi tiết:
Quan sát đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) ta thấy chúng là một đường nét liền trên \(\left( { - \infty ; + \infty } \right)\) nên hai hàm số đó liên tục trên \(\left( { - \infty ; + \infty } \right)\)
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} + x - 2}}{{x - 1}}\,\,\,khi\,\,x \ne 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,khi\,\,x = 1\end{array} \right.\) trên \(\mathbb{R}\)
Phương pháp giải:
Hàm số liên tục trên \(\mathbb{R}\) nếu nó liên tục tại mọi điểm thuộc \(\mathbb{R}\)
Hàm số phân thức hữu tỉ (thương của hai đa thức) liên tục trên từng khoảng xác định của chúng.
Xét tính liên tục của hàm số \(f\left( x \right)\) tại điểm \(x = 1\)
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\)
+ Trên tập \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\), hàm số \(f\left( x \right) = \frac{{{x^3} + x - 2}}{{x - 1}}\) là phân thức hữu tỉ xác định trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) nên liên tục trên các khoảng này.
+ Khi \(x = 1\), ta có \(f\left( 1 \right) = 2\).
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^3} + x - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {{x^2} + x + 2} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x + 2} \right) = {1^2} + 1 + 2 = 4 \ne f\left( 1 \right)\)
Vậy hàm số \(f\left( x \right)\) không liên tục tại \(x = 1\)
Suy ra hàm số đã cho gián đoạn tại \(x = 1\) hay hàm số \(f\left( x \right)\) không liên tục trên \(\mathbb{R}\)
Cho hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = \frac{1}{x}\).
a) Xét tính liên tục của \(y = f\left( x \right)\) và \(y = g\left( x \right)\) tại \({x_0} = 1\).
b) Xét tính liên tục của hàm số \(y = f\left( x \right) + g\left( x \right)\) tại \({x_0} = 1\).
Phương pháp giải:
Hàm số liên tại tại điểm \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Tính \(f\left( {{x_0}} \right)\) và \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) rồi so sánh chúng
Tương tự với hàm \(y = g\left( x \right)\) và \(y = f\left( x \right) + g\left( x \right)\)
Lời giải chi tiết:
a)
+ Hàm số \(y = f\left( x \right) = {x^2}\) có TXĐ là \(\mathbb{R}\)
Với \({x_0} = 1 \Rightarrow f\left( 1 \right) = {1^2} = 1\)
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} {x^2} = {1^2} = 1 = f\left( 1 \right)\). Suy ra, hàm số \(y = f\left( x \right)\) liên tục tại \({x_0} = 1\)
+ Hàm số \(y = g\left( x \right) = \frac{1}{x}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\)
Với \({x_0} = 1 \Rightarrow g\left( 1 \right) = \frac{1}{1} = 1\)
\(\mathop {\lim }\limits_{x \to 1} g\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{1}{x} = \frac{1}{1} = 1 = f\left( 1 \right)\). Suy ra, hàm số \(y = f\left( x \right)\) liên tục tại \({x_0} = 1\)
b) Với \({x_0} = 1 \Rightarrow f\left( 1 \right) + g\left( 1 \right) = {1^2} + \frac{1}{1} = 2\)
\(\mathop {\lim }\limits_{x \to 1} \left( {f\left( x \right) + g\left( x \right)} \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + \frac{1}{x}} \right) = {1^2} + \frac{1}{1} = 2 = f\left( 1 \right) + g\left( 1 \right)\).
Suy ra, hàm số \(y = f\left( x \right) + g\left( x \right)\) liên tục tại \({x_0} = 1\)
Tìm các khoảng trên đó hàm số sau đây là liên tục: \(y = x + \tan x\)
Phương pháp giải:
Hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) là các hàm số liên tục trên khoảng K thì hàm số \(y = f\left( x \right) \pm g\left( x \right)\) cũng liên tục trên khoảng K
Hàm số \(y = \tan x,y = \cot x\) liên tục trên từng khoảng xác định của chúng
Tìm tập xác định của hàm số
Lời giải chi tiết:
Xét hàm số \(f\left( x \right) = x\) và \(g\left( x \right) = \tan x\)
+ Hàm số \(f\left( x \right) = x\) là hàm đa thức nên \(f\left( x \right)\) liên tục trên \(\mathbb{R}\)
+ Hàm số \(g\left( x \right) = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\) nên hàm số \(g\left( x \right)\) liên tục trên các khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right)\)
Do đó, hàm số \(y = f\left( x \right) + g\left( x \right) = x + \tan x\) liên tục trên các khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right)\)
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x + 1\,\,khi\,\,x \le 0\\ax + b\,\,khi\,\,0 < x < 2\\4 - x\,\,\,khi\,\,2 \le x\end{array} \right.\), trong đó \(a\) và \(b\) là hai số thực. Tìm \(a\) và \(b\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Phương pháp giải:
Hàm số liên tục trên \(\mathbb{R}\) nếu nó liên tục tại mọi điểm thuộc \(\mathbb{R}\)
Dựa tính liên tục tại các điểm \(x = 0;x = 2\) để tìm \(a\) và \(b\)
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\)
Với \(x < 0\), hàm số \(f\left( x \right) = x + 1\) là hàm đa thức nên hàm số liên tục trên khoảng \(\left( { - \infty ;0} \right)\)
Với \(0 < x < 2\), hàm số \(f\left( x \right) = ax + b\) là hàm đa thức nên hàm số liên tục trên khoảng \(\left( {0;2} \right)\)
Với \(x > 2\), hàm số \(f\left( x \right) = 4 - x\) là hàm đa thức nên hàm số liên tục trên khoảng \(\left( {2; + \infty } \right)\)
Để hàm số liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại các điểm \(x = 0\) và \(x = 2\)
+ Với \(x = 0 \Rightarrow f\left( 0 \right) = 0 + 1 = 1\)
\(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {x + 1} \right) = 0 + 1 = 1\)
\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {ax + b} \right) = a.0 + b = b\)
Để hàm số liên tục tại \(x = 0\) thì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) \Leftrightarrow b = 1\) \(\left( 1 \right)\)
+ Với \(x = 2 \Rightarrow f\left( 2 \right) = 4 - 2 = 2\)
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {ax + b} \right) = 2a + b\)
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {4 - x} \right) = 4 - 2 = 2\)
Để hàm số liên tục tại \(x = 2\) thì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = f\left( 2 \right) \Leftrightarrow 2a + b = 2\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(\left\{ \begin{array}{l}b = 1\\2a + b = 2\end{array} \right. \Leftrightarrow a = \frac{1}{2};b = 1\)
Mục 2 của SGK Toán 11 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm, định lý và phương pháp đã được học. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và giải thích rõ ràng để giúp các em hiểu rõ bản chất của vấn đề.
Bài tập 1 thường là bài tập áp dụng trực tiếp các kiến thức đã học. Để giải bài tập này, các em cần:
Ví dụ, nếu bài tập yêu cầu tính giới hạn của một hàm số, các em cần sử dụng các quy tắc tính giới hạn đã học. Lời giải chi tiết sẽ được trình bày từng bước để các em dễ dàng theo dõi.
Bài tập 2 có thể là bài tập nâng cao hơn, đòi hỏi các em phải vận dụng linh hoạt các kiến thức đã học và có khả năng tư duy logic. Để giải bài tập này, các em cần:
Lời giải chi tiết sẽ được trình bày với các bước giải thích rõ ràng, giúp các em hiểu được cách tiếp cận và giải quyết bài toán.
Bài tập 3 có thể là bài tập tổng hợp, kết hợp nhiều kiến thức khác nhau. Để giải bài tập này, các em cần:
Lời giải chi tiết sẽ được trình bày một cách logic và dễ hiểu, giúp các em nắm vững phương pháp giải quyết bài toán.
Để đạt kết quả tốt nhất khi giải bài tập mục 2 trang 83, 84 SGK Toán 11 tập 1, các em cần lưu ý:
Kiến thức trong mục 2 trang 83, 84 SGK Toán 11 tập 1 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Việc nắm vững kiến thức này sẽ giúp các em có nền tảng vững chắc để học tập và làm việc trong tương lai.
Hy vọng rằng bài viết này đã cung cấp cho các em những thông tin hữu ích và giúp các em giải quyết các bài tập trong mục 2 trang 83, 84 SGK Toán 11 tập 1 một cách hiệu quả. Chúc các em học tập tốt!