Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 3 trang 47, 48, 49 của sách giáo khoa Toán 11 tập 1.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) mà \({u_n} = 1 + \frac{1}{n}\) và \({v_n} = 2 - \frac{1}{n}\) (n là số nguyên dương).
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) mà \({u_n} = 1 + \frac{1}{n}\) và \({v_n} = 2 - \frac{1}{n}\) (n là số nguyên dương).
a) So sánh \({u_{n + 1}}\) và \({u_n}\).
b) So sánh \({v_{n + 1}}\) và \({v_n}\).
Phương pháp giải:
Thay n = n + 1 vào công thức tổng quát của dãy số. So sánh \({u_{n + 1}} - {u_n}\), \({v_{n + 1}} - {v_n}\) với 0.
Lời giải chi tiết:
a) Ta có: \({u_{n + 1}} - {u_n} = 1 + \frac{1}{{n + 1}} - 1 - \frac{1}{n} = \frac{1}{{n + 1}} - \frac{1}{n} = \frac{{n - \left( {n + 1} \right)}}{{n\left( {n + 1} \right)}} = \frac{ -1}{{n\left( {n + 1} \right)}}\)
Mà n là số nguyên dương nên \(\frac{ -1}{{n\left( {n + 1} \right)}} < 0\)\( \Rightarrow {u_{n + 1}} - {u_n} < 0 \Rightarrow {u_{n + 1}} < {u_n}\).
b) Ta có: \({v_{n + 1}} - {v_n} = 2 - \frac{1}{{n + 1}} - 2 + \frac{1}{n} = \frac{1}{n} - \frac{1}{{n + 1}} = \frac{{n + 1 - n}}{{n\left( {n + 1} \right)}} = \frac{1}{{n\left( {n + 1} \right)}}\)
Mà n là số nguyên dương nên \(\frac{1}{{n\left( {n + 1} \right)}} > 0 \Rightarrow {v_{n + 1}} - {v_n} > 0 \Rightarrow {v_{n + 1}} > {v_n}\).
Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) cho bởi \({u_n} = \frac{{n - 2}}{{3n - 1}},\forall n \in {\mathbb{N}^*}\) là một dãy số tăng.
Phương pháp giải:
So sánh \({u_{n + 1}}\) và \({u_n}\). Nếu \({u_{n + 1}} > {u_n}\forall n\) thì là dãy số tăng.
Lời giải chi tiết:
\(\begin{array}{l}{u_{n + 1}} = \frac{{n + 1 - 2}}{{3(n + 1) - 1}} = \frac{{n - 1}}{{3n + 2}}\\{u_{n + 1}} - {u_n} = \frac{{n - 1}}{{3n + 2}} - \frac{{n - 2}}{{3n - 1}} = \frac{5}{{9{n^2} + 3n - 2}}\\9{n^2} + 3n - 2 > 0\forall n \ge 1 \Rightarrow \frac{5}{{9{n^2} + 3n - 2}} > 0\\ \Rightarrow {u_{n + 1}} - {u_n} > 0\end{array}\)
\(\Rightarrow {u_{n + 1}} > {u_n}\forall n\)
Vậy dãy số đã cho là một dãy số tăng.
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{\sqrt n }}{{n + 1}}\)
a) So sánh n + 1 và \(2\sqrt n \) .
b) Suy ra: \({u_n} \le \frac{1}{2}\), với mọi số nguyên dương n.
Phương pháp giải:
a) So sánh \(n + 1 - 2\sqrt n \) với 0.
b) Áp dụng phần a.
Lời giải chi tiết:
a) \(n + 1 - 2\sqrt n = {\left( {\sqrt n - 1} \right)^2} \ge 0\forall n \Rightarrow n + 1 \ge 2\sqrt n \)
b) \(n + 1 \ge 2\sqrt n \Rightarrow \frac{{\sqrt n }}{{n + 1}} \le \frac{{\sqrt n }}{{2\sqrt n }} = \frac{1}{2} \Rightarrow {u_n} = \frac{1}{2}\forall n\) nguyên dương
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{n - 1}}{{n + 2}}\), với n là số nguyên dương.
a) Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) tăng.
b) Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) bị chặn.
Phương pháp giải:
a) So sánh \({u_{n + 1}}\) và \({u_n}\). Nếu \({u_{n + 1}} > {u_n}\forall n\) thì là dãy số tăng.
b) Dãy số \(\left( {{u_n}} \right)\) bị chặn khi \(m \le {u_n} \le M\forall n\) nguyên dương.
Lời giải chi tiết:
a)
\(\begin{array}{l}{u_n} = \frac{{n - 1}}{{n + 2}} = 1 - \frac{3}{{n + 2}}\\{u_{n + 1}} - {u_n} = 1 - \frac{3}{{n + 3}} - \left( {1 - \frac{3}{{n + 2}}} \right) = \frac{3}{{n + 2}} - \frac{3}{{n + 3}} = 3\left( {\frac{1}{{n + 2}} - \frac{1}{{n + 3}}} \right)\\n + 2 < n + 3 \Rightarrow \frac{1}{{n + 2}} > \frac{1}{{n + 3}} \Leftrightarrow \frac{1}{{n + 2}} - \frac{1}{{n + 3}} > 0 \Leftrightarrow 3\left( {\frac{1}{{n + 2}} - \frac{1}{{n + 3}}} \right) > 0\\ \Rightarrow {u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\end{array}\)
Vậy dãy số đã cho là dãy số tăng.
b) n là số nguyên dương \( \Rightarrow n \ge 1 \Leftrightarrow \left\{ \begin{array}{l}n - 1 \ge 0\\n + 2 > 0\end{array} \right. \Leftrightarrow \frac{{n - 1}}{{n + 2}} \ge 0\)
\(n - 1 < n + 2 \Rightarrow \frac{{n - 1}}{{n + 2}} < 1\)
\( \Rightarrow 0 \le \frac{{n - 1}}{{n + 2}} < 1\forall n\) nguyên dương
Vậy dãy số đã cho là dãy số bị chặn.
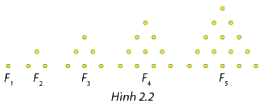
Trong một trò chơi của trẻ em, các em nhỏ dùng các viên bi để xếp thành các hình tam giác Fn. Dãy các hình xếp (Fn) tuân theo một quy luật được mô tả trong Hình 2.2. Trong đó F1 chỉ có 1 viên bi, thêm 2 viên bi để được tam giác đều là hình F2, thêm 3 viên bi thẳng hàng và song song với một cạnh của F2 để được tam giác đều F3,… Gọi (un) là dãy số mà un là số viên bi cần dùng để xếp được hình Fn \(\left( {n \in {\mathbb{N}^*}} \right)\). Chẳng hạn \({u_1} = 1,{u_2} = 3,{u_3} = 6\),…
a) Viết sáu số hạng đầu tiên của dãy số (un).
b) Dự đoán công thức truy hồi để tính un.
Phương pháp giải:
Số hạng đứng sau hơn số hạng đứng trước đúng một số bằng số thứ tự của số hạng đứng sau.
Lời giải chi tiết:
a) \({u_1} = 1,{u_2} = 3,{u_3} = 6,{u_4} = 6 + 4 = 10,{u_5} = 10 + 5 = 15,{u_6} = 15 + 6 = 21\)
b) Công tính truy hồi: \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = {u_n} + n + 1\end{array} \right.\)
Mục 3 trong SGK Toán 11 tập 1 thường tập trung vào một chủ đề cụ thể, ví dụ như hàm số bậc hai, phương trình bậc hai, hoặc các ứng dụng của đạo hàm. Việc nắm vững kiến thức lý thuyết và kỹ năng giải bài tập trong mục này là rất quan trọng để xây dựng nền tảng vững chắc cho các kiến thức tiếp theo.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về định nghĩa hàm số, tập xác định, tập giá trị để xác định các yếu tố của hàm số cho trước. Ví dụ, cho hàm số f(x) = x^2 - 4x + 3, hãy xác định tập xác định và tập giá trị của hàm số.
Bài tập này có thể yêu cầu học sinh vẽ đồ thị hàm số, tìm điểm uốn, điểm cực trị, hoặc khảo sát sự biến thiên của hàm số. Để giải bài tập này, học sinh cần nắm vững các phương pháp vẽ đồ thị hàm số và các công thức tính đạo hàm.
Bài tập này thường liên quan đến việc giải phương trình, bất phương trình, hoặc hệ phương trình. Học sinh cần áp dụng các phương pháp giải phương trình, bất phương trình đã học để tìm ra nghiệm của phương trình.
Bài tập này có thể là một bài toán thực tế, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết vấn đề. Ví dụ, một người nông dân muốn xây một hàng rào bao quanh một khu vườn hình chữ nhật có diện tích nhất định. Hỏi người nông dân cần sử dụng bao nhiêu mét hàng rào để tiết kiệm chi phí nhất?
Bài tập: Giải phương trình x^2 - 5x + 6 = 0
Lời giải:
Phương trình x^2 - 5x + 6 = 0 có dạng ax^2 + bx + c = 0 với a = 1, b = -5, c = 6.
Tính delta: Δ = b^2 - 4ac = (-5)^2 - 4 * 1 * 6 = 25 - 24 = 1
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + 1) / 2 = 3
x2 = (-b - √Δ) / 2a = (5 - 1) / 2 = 2
Vậy, phương trình x^2 - 5x + 6 = 0 có hai nghiệm là x1 = 3 và x2 = 2.
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 3 trang 47, 48, 49 SGK Toán 11 tập 1. Chúc các em học tập tốt và đạt kết quả cao!