Bài 5.6 trang 134 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc giải các phương trình lượng giác cơ bản. Bài tập này giúp học sinh rèn luyện kỹ năng biến đổi lượng giác và áp dụng các công thức lượng giác đã học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 5.6 trang 134, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một viện nghiên cứu nuôi trồng thủy sản triển khai nuôi thí điểm giống cá mới ở hai cơ sở A, B theo hai phương pháp khác nhau.
Đề bài
Một viện nghiên cứu nuôi trồng thủy sản triển khai nuôi thí điểm giống cá mới ở hai cơ sở A, B theo hai phương pháp khác nhau. Sau ba tháng, mỗi cơ sở kiểm tra lại khối lượng của một số cá. Số liệu dưới đây được gửi về viện nghiên cứu
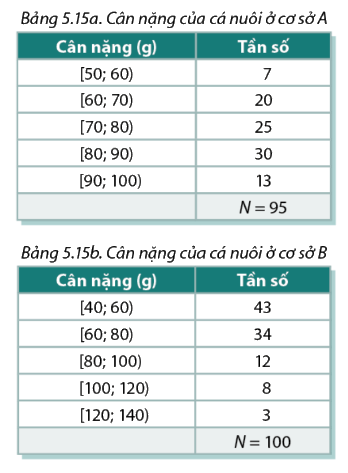
Hãy ước tính khối lượng trung bình của cá nuôi ở mỗi cơ sở. Nhà nghiên cứu có thể đứa ra kết luận gì về hiệu quả của hai phương pháp nuôi cá.
Phương pháp giải - Xem chi tiết
Lập bảng mẫu số liệu ghép nhóm của từng cơ sở sau đó tính giá trị trung bình và thực hiện so sánh.
Lời giải chi tiết
Bảng mẫu số liệu ghép nhóm cân nặng của cá nuôi ở cơ sở A
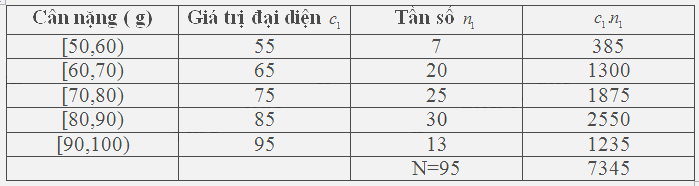
Cân nặng trung bình của cá nuôi ở cơ sở A là: \(\mathop {{x_A}}\limits^\_ = \frac{{7345}}{{95}} = 77,31\) (g)
Bảng mẫu số liệu ghép nhóm cân nặng của cá nuôi ở cơ sở B
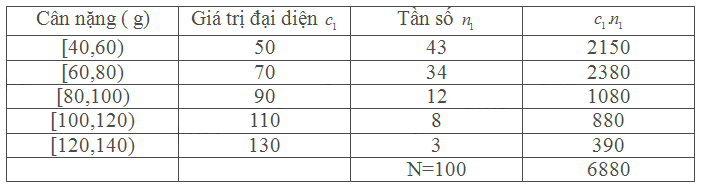
Cân nặng trung bình của cá nuôi ở cơ sở B là: \(\mathop {{x_B}}\limits^\_ = \frac{{6880}}{{100}} = 68,8\) (g)
Do \({x_B} < {x_A}\) nên phương pháp nuôi của công ty A tốt hơn.
Bài 5.6 trang 134 SGK Toán 11 tập 1 yêu cầu giải các phương trình lượng giác sau:
Phương trình sin(x) = 1/2 có nghiệm là:
Giải thích:
Ta biết rằng sin(π/6) = 1/2. Do đó, một nghiệm của phương trình là x = π/6. Vì sin(x) = sin(π - x), nên nghiệm còn lại là x = π - π/6 = 5π/6. Hàm sin có chu kỳ 2π, nên ta cộng k2π vào cả hai nghiệm để được nghiệm tổng quát.
Phương trình cos(x) = -√3/2 có nghiệm là:
Giải thích:
Ta biết rằng cos(5π/6) = -√3/2. Do đó, một nghiệm của phương trình là x = 5π/6. Vì cos(x) = cos(-x), nên nghiệm còn lại là x = -5π/6 + 2π = 7π/6. Hàm cos có chu kỳ 2π, nên ta cộng k2π vào cả hai nghiệm để được nghiệm tổng quát.
Phương trình tan(x) = 1 có nghiệm là:
Giải thích:
Ta biết rằng tan(π/4) = 1. Hàm tan có chu kỳ π, nên ta cộng kπ vào nghiệm để được nghiệm tổng quát.
Phương trình cot(x) = 0 có nghiệm là:
Giải thích:
Cot(x) = 1/tan(x). Cot(x) = 0 khi tan(x) tiến tới vô cùng, điều này xảy ra khi x = π/2 + kπ. Hàm cot có chu kỳ π, nên ta cộng kπ vào nghiệm để được nghiệm tổng quát.
Giải phương trình lượng giác có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
Việc nắm vững kiến thức về phương trình lượng giác là rất quan trọng đối với học sinh THPT và những người làm việc trong các lĩnh vực liên quan đến khoa học và kỹ thuật.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải bài 5.6 trang 134 SGK Toán 11 tập 1 và các bài tập tương tự. Chúc các bạn học tốt!