Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 135, 136 SGK Toán 11 tập 1 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho các em học sinh trên con đường chinh phục môn Toán.
Bảng 5.16 là bảng tần số ghép nhóm về chiều cao của 50 học sinh
Bảng 5.16 là bảng tần số ghép nhóm về chiều cao của 50 học sinh
a, Nếu mẫu số liệu lúc chưa ghép nhóm được sắp xếp thành dãy không giảm , kí hiệu \({u_1},{u_2},...,{u_{50}}\)thì trung vị được tính như thế nào?
b, Xác định nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\), với N là cỡ mẫu .
Hãy chứng minh trung vị thuộc nhóm ghép này
Phương pháp giải:
a, Trung vị là số hạng đứng giữa của dãy số.
b, Lập bảng tần số tích lũy cho mẫu số liệu ghép nhóm
Lời giải chi tiết:
a, Trung vị là số hạng \({u_{25}}\) của dãy số đã cho.
b, Bảng tần số tích lũy của mẫu số liệu ghép nhóm chiều cao của 50 học sinh
Ta có : \(\frac{N}{2} = \frac{{50}}{2} = 25\).Nhóm có tần số tích lũy lớn hơn 25 là [158,161)
Do trung vị là số hạng thứ 25 của dãy số nên nhóm chứa trung vị là nhóm đầu tiên có tần số tích lũy lớn hơn 25.
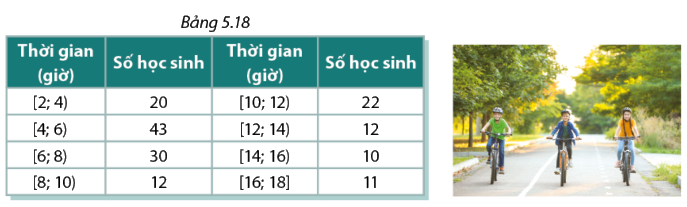
Trong cuộc vận động sử dụng xe đạp làm phương tiện giao thông để nâng cao sức khỏe và góp phần bảo vệ môi trường, nhà trường đã tìm hiểu thời gian đi xe đạp trong một tháng của một số học sinh. Kết quả điều tra biểu diễn bới Bảng 5.18 . Hãy xác định nhóm chứa trung vị của mẫu số liệu.

Phương pháp giải:
Lập bảng tần số tích lũy của mẫu số liệu ghép nhóm thời gian đi xe đạp của học sinh
Lời giải chi tiết:
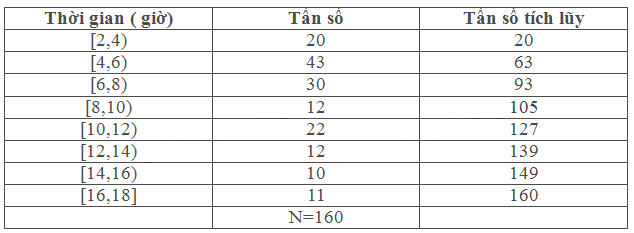
Bảng tần số tích lũy mẫu số liệu ghép nhóm thời gian đi xe đạp của học sinh

Ta có: \(\frac{N}{2} = \frac{{160}}{2} = 80\). Vậy nhóm chứa trung vị là nhóm [6,8) ( do tần số tích lũy nhóm này là 93 > 80).
Mục 1 trang 135, 136 SGK Toán 11 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào từng bài tập, phân tích yêu cầu đề bài và đưa ra lời giải chi tiết, kèm theo các lưu ý quan trọng.
Để đảm bảo tính chính xác và dễ hiểu, chúng ta sẽ xem xét từng bài tập cụ thể trong mục 1 trang 135, 136 SGK Toán 11 tập 1. (Giả sử các bài tập là về phép biến hình affine)
Bài tập này yêu cầu học sinh xác định xem một phép biến hình cho trước có phải là phép biến hình affine hay không. Để làm được điều này, học sinh cần kiểm tra xem phép biến hình đó có bảo toàn thẳng và bảo toàn collinearity hay không. Một phép biến hình affine là một phép biến hình bảo toàn collinearity (tức là ba điểm thẳng hàng thì ảnh của chúng cũng thẳng hàng) và bảo toàn tỷ số khoảng cách giữa các điểm trên cùng một đường thẳng.
Bài tập này yêu cầu học sinh tìm tọa độ của ảnh của một điểm cho trước qua một phép biến hình affine. Để làm được điều này, học sinh cần áp dụng công thức của phép biến hình affine. Công thức tổng quát của phép biến hình affine là: x' = ax + by + c và y' = dx + ey + f, trong đó (x, y) là tọa độ của điểm ban đầu và (x', y') là tọa độ của điểm ảnh.
Bài tập này yêu cầu học sinh chứng minh một tính chất nào đó liên quan đến phép biến hình affine. Để làm được điều này, học sinh cần sử dụng các định lý và tính chất đã học về phép biến hình affine. Ví dụ, chứng minh rằng ảnh của một đường thẳng qua phép biến hình affine vẫn là một đường thẳng.
Ví dụ: Cho phép biến hình affine f(x, y) = (2x + y, x - y). Tìm ảnh của điểm A(1, 2) qua phép biến hình f.
Giải: Áp dụng công thức của phép biến hình affine, ta có:
x' = 2(1) + 2 = 4
y' = 1 - 2 = -1
Vậy, ảnh của điểm A(1, 2) qua phép biến hình f là A'(4, -1).
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể tự giải thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kinh nghiệm và học hỏi lẫn nhau.
Hy vọng rằng bài giải chi tiết mục 1 trang 135, 136 SGK Toán 11 tập 1 trên giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về phép biến hình affine và tự tin hơn trong quá trình học tập. Chúc các em học tốt!