Bài 2.20 trang 56 SGK Toán 11 tập 1 thuộc chương 1: Hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng và các điểm đặc biệt để giải quyết các bài toán liên quan đến hàm số bậc hai.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
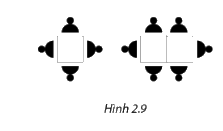
Trong một nhà hàng, một bàn vuông ngồi được 4 người, nếu nối hai bàn vuông lại thì ngồi được 6 người, nối ba bàn ngồi được 8 người, ... Nếu nối n bàn vuông lại theo một hàng ngang thì ngồi được bao nhiêu người?
Đề bài
Trong một nhà hàng, một bàn vuông ngồi được 4 người, nếu nối hai bàn vuông lại thì ngồi được 6 người, nối ba bàn ngồi được 8 người, ... Nếu nối n bàn vuông lại theo một hàng ngang thì ngồi được bao nhiêu người?
Phương pháp giải - Xem chi tiết
Mỗi khi nối thêm 1 bàn thì có thể ngồi thêm 2 người. Từ đó lập cấp số cộng.
Áp dụng công thức \({u_{n + 1}} = {u_1}.{q^n}\) để tính số người khi nối n bàn với nhau.
Lời giải chi tiết
Gọi số người khi ngồi một bàn, khi nối hai bàn, khi nối ba bàn lần lượt là \({u_1},{u_2},{u_3}\).
\( \Rightarrow {u_1} = 4,{u_2} = 6,{u_3} = 8\)
\( \Rightarrow d = {u_2} - {u_1} = 2\)
Ta lập được cấp số cộng với \({u_1} = 4,d = 8\).
Vậy khi nối n bàn lại với nhau thì ngồi được \({u_n} = {u_1} + \left( {n - 1} \right)d = 4 + \left( {n - 1} \right).2 = 2n + 2\) (người).
Bài 2.20 trang 56 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc hiểu và vận dụng các tính chất của hàm số bậc hai. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Nội dung bài tập: Bài 2.20 thường yêu cầu học sinh xác định các yếu tố của parabol (đỉnh, trục đối xứng, điểm thuộc parabol) dựa vào phương trình hàm số bậc hai đã cho. Hoặc, bài tập có thể yêu cầu học sinh tìm phương trình hàm số bậc hai khi biết một số thông tin về parabol (ví dụ: đỉnh, trục đối xứng, ba điểm thuộc parabol).
Phương pháp giải:
Ví dụ minh họa:
Giả sử cho hàm số y = 2x2 - 4x + 1.
Lưu ý:
Ứng dụng thực tế:
Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:
Kết luận:
Bài 2.20 trang 56 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc hai và các ứng dụng của nó. Bằng cách nắm vững các khái niệm cơ bản, phương pháp giải và rèn luyện thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và áp dụng kiến thức vào thực tế.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ học tập tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi.