Chào mừng các em học sinh đến với bài giải chi tiết mục 4 trang 62 SGK Toán 11 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Bài tập trong mục này tập trung vào các kiến thức về... (phần này cần được điền kiến thức cụ thể của mục 4)
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot \left( {ABCD} \right)\).
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot \left( {ABCD} \right)\).
a) Tìm hình chiếu \(d\) của \(A'C\) trên mặt phẳng \(\left( {ABCD} \right)\). Xác định góc giữa \(A'C\) và \(d\)
b) Tìm hình chiếu \(a\) của \(A'C'\) trên mặt phẳng \(\left( {ABCD} \right)\). Xác định góc giữa \(A'C'\) và \(a\)
Phương pháp giải:
a) Chứng minh \(A'A \bot \left( {ABCD} \right)\) từ đó suy ra \(A'\) là hình chiếu của \(A\) trên \(\left( {ABCD} \right)\)
b) Chứng minh \(CC' \bot \left( {ABCD} \right)\) từ đó suy ra \(C'\) là hình chiếu của \(C\) trên \(\left( {ABCD} \right)\)
Lời giải chi tiết:
a) Vì \(A'A \bot \left( {ABCD} \right)\) nên \(A\) là hình chiếu của \(A'\) trên \(\left( {ABCD} \right)\)
Vậy hình chiếu \(d\) của \(A'C\) trên \(\left( {ABCD} \right)\) là \(AC\)
Góc giữa \(A'C\) và \(AC\) là góc \(\widehat {A'CA}\)
b) Vì \(A'A \bot \left( {ABCD} \right)\) nên \(A\) là hình chiếu của \(A'\) trên \(\left( {ABCD} \right)\)
Vì \(CC' \bot \left( {ABCD} \right)\) nên \(C\) là hình chiếu của \(C'\) trên \(\left( {ABCD} \right)\)
Vậy hình chiếu \(a\) của \(A'C'\) trên \(\left( {ABCD} \right)\) là \(AC\)
Vì \(A'C'//AC\) nên góc giữa \(A'C'\) và \(AC\) bằng \({0^o}\)
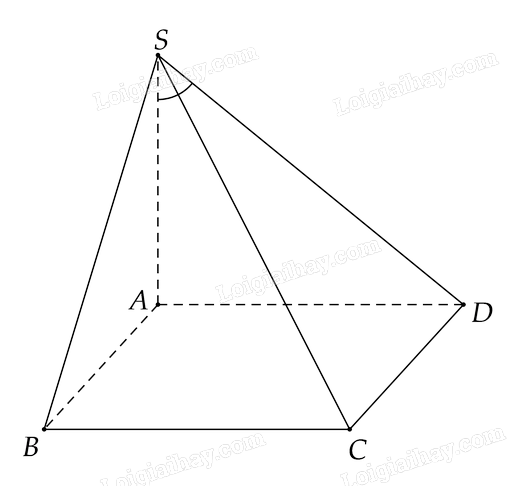
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\), \(SA = a\sqrt 3 \). Xác định và tính góc giữa đường thẳng \(SD\) và \(\left( {SAB} \right)\)
Phương pháp giải:
Xác định giao điểm \(S\) của \(SD\) và \(\left( {SAB} \right)\)
Chứng minh \(DA \bot \left( {SAB} \right)\) từ đó suy ra \(SA\) là hình chiếu vuông góc của \(SD\) trên \(\left( {SAB} \right)\) suy ra góc cần tìm là góc giữa 2 đường thẳng \(SD\) và \(SA\)
Sử dụng tỉ số lượng giác trong tam giác vuông
Lời giải chi tiết:

Ta có \(S\) là giao điểm của \(SD\) và \(\left( {SAB} \right)\) \(\left( 1 \right)\)
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD\).
Vì \(ABCD\) là hình vuông lên \(AD \bot AB\)
Ta có \(\left\{ \begin{array}{l}AD \bot SA\\AD \bot AB\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right) \Rightarrow \)\(A\) là hình chiếu vuông góc của \(D\) trên \(\left( {SAB} \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(SA\) là hình chiếu vuông góc của \(SD\) trên \(\left( {SAB} \right)\)
Vậy góc giữa \(SD\) và \(\left( {SAB} \right)\) là góc giữa \(SA\) và \(SD\) là góc giữa \(\widehat {DSA}\)
Xét \(\Delta SAD\) vuông tại \(A\) có \(\tan S = \frac{{AD}}{{SA}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {ASD} = {30^o}\)
Mục 4 trang 62 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để đạt kết quả tốt trong môn học này.
Mục 4 thường bao gồm các dạng bài tập liên quan đến... (Liệt kê các dạng bài tập chính của mục 4, ví dụ: phương trình lượng giác cơ bản, giải phương trình lượng giác nâng cao, ứng dụng của phương trình lượng giác vào thực tế...). Các bài tập này đòi hỏi học sinh phải có khả năng phân tích đề bài, lựa chọn phương pháp giải phù hợp và thực hiện các phép tính chính xác.
Bài 1: (Đề bài cụ thể của bài tập 1)
Lời giải: (Giải chi tiết bài tập 1, bao gồm các bước biến đổi, áp dụng công thức và kết luận)
Bài 2: (Đề bài cụ thể của bài tập 2)
Lời giải: (Giải chi tiết bài tập 2, bao gồm các bước biến đổi, áp dụng công thức và kết luận)
Kiến thức về phương trình lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực của khoa học và kỹ thuật, như vật lý, kỹ thuật điện, xử lý tín hiệu... Ví dụ, trong vật lý, phương trình lượng giác được sử dụng để mô tả các hiện tượng dao động, sóng...
Để hiểu sâu hơn về kiến thức trong Mục 4 trang 62, các em có thể tham khảo thêm các tài liệu sau:
Giải mục 4 trang 62 SGK Toán 11 tập 2 đòi hỏi sự nắm vững kiến thức lý thuyết, kỹ năng biến đổi đại số và khả năng áp dụng vào thực tế. Hy vọng với bài giải chi tiết và các phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn trong việc giải quyết các bài tập Toán 11.