Bài 8.30 trang 83 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm đạo hàm, quy tắc tính đạo hàm và cách sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho Bài 8.30 trang 83 SGK Toán 11 tập 2, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A
Đề bài
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều các điểm A, B, C. Biết AA’ = 2a, tính thể tích khối lăng trụ này.
Phương pháp giải - Xem chi tiết
Công thức tính thể tích hình lăng trụ: V = S.h với S là diện tích đáy, h là chiều cao.
Lời giải chi tiết
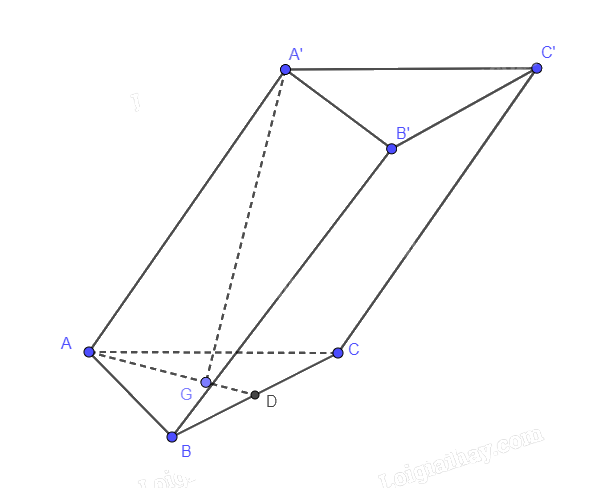
Gọi D là trung điểm của AC, G là trọng tâm tam giác ABC
A’.ABC là chóp tam giác đều nên A’G vuông góc với (ABC). Suy ra A’G là chiều cao của hình lăng trụ
Tam giác ABC đều có cạnh bằng a nên BD vuông góc với AC
Ta có: \(BD = \sqrt {A{B^2} - A{D^2}} = \sqrt {{a^2} - {{\left( {\frac{1}{2}a} \right)}^2}} = \frac{{\sqrt 3 }}{2}a\)
\(BG = \frac{2}{3}BD = \frac{{\sqrt 3 }}{3}a\)
Xét tam giác vuông A’BG vuông tại G có:
\(A'G = \sqrt {A'{B^2} - B{G^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\frac{{\sqrt 3 }}{3}a} \right)}^2}} = \frac{{\sqrt {33} }}{3}a\)
\(V = S.h = \frac{1}{2}.BD.AC.A'G = \frac{1}{2}.\frac{{\sqrt 3 }}{2}a.a.\frac{{\sqrt {33} }}{3}a = \frac{{\sqrt {11} }}{4}{a^3}\)
Bài 8.30 trang 83 SGK Toán 11 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến việc tối ưu hóa một đại lượng nào đó bằng cách sử dụng đạo hàm. Để giải bài toán này, học sinh cần thực hiện các bước sau:
Giả sử bài toán yêu cầu tìm kích thước của một hình hộp chữ nhật có thể tích cho trước sao cho diện tích bề mặt nhỏ nhất. Ta có thể giải bài toán này bằng cách:
Khi giải Bài 8.30 trang 83 SGK Toán 11 tập 2, học sinh cần lưu ý một số điểm sau:
Đạo hàm là một công cụ mạnh mẽ trong việc giải các bài toán tối ưu hóa. Nó cho phép ta tìm ra các điểm cực trị của hàm số, từ đó xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng xác định. Ứng dụng của đạo hàm trong giải Bài 8.30 trang 83 SGK Toán 11 tập 2 không chỉ giúp học sinh rèn luyện kỹ năng giải toán mà còn giúp họ hiểu rõ hơn về ứng dụng thực tế của đạo hàm trong các lĩnh vực khác nhau.
Ngoài ra, việc nắm vững kiến thức về đạo hàm còn là nền tảng quan trọng để học sinh tiếp thu các kiến thức nâng cao hơn về giải tích trong các lớp học tiếp theo.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn cam kết giúp học sinh học Toán hiệu quả và đạt kết quả cao.
Học sinh có thể truy cập Giaitoan.edu.vn để tìm hiểu thêm về Bài 8.30 trang 83 SGK Toán 11 tập 2 và các bài tập khác trong chương trình học Toán 11.