Bài 8.14 trang 72 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, \(SA \bot \left( {ABCD} \right)\). Biết số đo của góc nhị diện \(\left[ {S,BD,A} \right]\) bằng 450, tính chiều cao của hình chóp.
Đề bài
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, \(SA \bot \left( {ABCD} \right)\). Biết số đo của góc nhị diện \(\left[ {S,BD,A} \right]\) bằng 450, tính chiều cao của hình chóp.
Phương pháp giải - Xem chi tiết
Cách tìm số đo của góc nhị diện \(\left[ {S,CD,A} \right]\):
+ Tìm giao tuyến d của (SCD) và (ACD).
+ Tìm \(a \subset \left( {SCD} \right)\) vuông góc với d. Tìm \(b \subset \left( {ACD} \right)\) vuông góc với d.
+ Tính \(\left( {a,b} \right)\).
Lời giải chi tiết
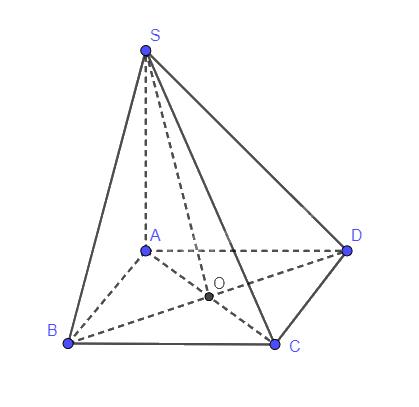
SA vuông góc với BD (Vì SA vuông góc với (ABCD))
AC vuông với BD (Vì ABCD là hình vuông)
Nên (SAC) vuông với BD
Trong (ABCD), gọi O là giao điểm của AC và BD
Suy ra SO vuông góc với BD
Mà: AO vuông góc với BD
Suy ra góc phẳng nhị diện \(\left[ {S,BD,A} \right]\) là góc SOA
Hình vuông ABCD có cạnh 2a nên AC = \(2\sqrt 2 a\). Suy ra AO = \(\sqrt 2 a\)
\(\tan \widehat {SOA} = \,\frac{{SA}}{{AO}} \Leftrightarrow \tan {45^0} = \frac{{SA}}{{\sqrt 2 a}} \Leftrightarrow SA = \sqrt 2 a\)
Bài 8.14 trang 72 SGK Toán 11 tập 2 yêu cầu học sinh giải một bài toán cụ thể liên quan đến việc tìm cực trị của hàm số. Để giải bài toán này, chúng ta cần thực hiện các bước sau:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Bước 5: Kết luận: Hàm số đạt cực đại tại x = 0, f(0) = 2 và đạt cực tiểu tại x = 2, f(2) = -2.
Ngoài bài 8.14, SGK Toán 11 tập 2 còn nhiều bài tập tương tự về cực trị hàm số. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững kiến thức về đạo hàm, đạo hàm cấp hai và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Ngoài việc giải các bài tập trong SGK, học sinh có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, chẳng hạn như trong kinh tế, vật lý, kỹ thuật,... Đạo hàm là một công cụ mạnh mẽ giúp chúng ta phân tích và giải quyết nhiều vấn đề trong cuộc sống.
Việc hiểu rõ và vận dụng linh hoạt các kiến thức về đạo hàm sẽ giúp học sinh đạt kết quả tốt trong môn Toán 11 và chuẩn bị tốt cho các kỳ thi quan trọng.
giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải chi tiết và tài liệu học tập hữu ích.