Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau khám phá và giải chi tiết các bài tập trong mục 1 trang 73 và 74 của sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Cho đường thẳng a và một điểm O không thuộc a. H là hình chiếu của O trên đường thẳng a và M là một điểm bất kì thuộc a (Hình 8.49).
Cho đường thẳng a và một điểm O không thuộc a. H là hình chiếu của O trên đường thẳng a và M là một điểm bất kì thuộc a (Hình 8.49). Trong hai điểm H và M điểm nào có khoảng cách đến O ngắn hơn? Vì sao?
Phương pháp giải:
Quan hệ giữa đường xiên và hình chiếu.
Lời giải chi tiết:
Trong điểm H và M thì điểm H gần O hơn.
Vì tam giác OHM vuông tại H nên ta có OH < OM (quan hệ giữa đường xiên và hình chiếu)
Cho hình lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC. Tính khoảng cách từ G đến đường thẳng A’C’.
Phương pháp giải:
Cho O không thuộc a. H là hình chiếu của O trên a. Độ dài OH là khoảng cách từ O đến a.
Lời giải chi tiết:

Gọi G’ là trọng tâm tam giác A’B’C’, M là trung điểm AC, M’ là trung điểm của A’C’
Ta có: GG’ vuông góc với (A’B’C’) nên GG’ vuông góc với A’C’
G’M’ là trung tuyến của A’B’C’ nên G’M’ vuông góc với A’C’ (Vì tam giác A’B’C’ đều)
Suy ra (GG’M’) vuông góc với A’C’
\( \Rightarrow \)GM’ vuông góc với A’C’
Vậy GM’ là khoảng cách từ G đến A’C’
Tam giác A’B’C’ đều cạnh a nên B’M’ = \(B'M' = \frac{{\sqrt 3 }}{2}a\)
Suy ra G’M’ = \(G'M' = \frac{{\sqrt 3 }}{6}a\)
Xét tam giác vuông GM’G’ tại M’ có:
\(GM' = \sqrt {GG{'^2} + G'M{'^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{{\sqrt 3 }}{6}a} \right)}^2}} = \frac{{7\sqrt 3 }}{6}a\)
Cho mặt phẳng \(\left( \alpha \right)\) và O là một điểm không thuộc \(\left( \alpha \right)\). H là hình chiếu của O trên \(\left( \alpha \right)\). Lấy tuy ý điểm M thuộc \(\left( \alpha \right)\). Trong các diểm H và M, điểm nào có khoảng cách đến O ngắn hơn? Vì sao?

Phương pháp giải:
Quan hệ đường xiên và hình chiếu.
Lời giải chi tiết:
Tam giác OHM vuông tại H nên OH < OM (Quan hệ đường xiên và hình chiếu).
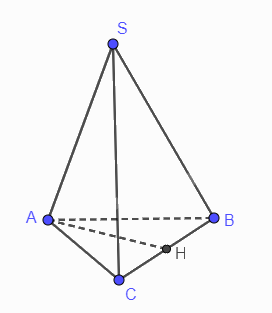
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = 2a; tam giác ABC đều bằng a. Tính khoảng cách từ A đến mặt phẳng (SBC).
Phương pháp giải:
Tìm khoảng cách từ M đến (P):
+ Tìm (Q) chứa M và vuông góc với (P) theo giao tuyến d.
+ Từ M hạ MH vuông góc với d (H thuộc d).
+ Khi đó MH chính là khoảng cách cần tìm.
Lời giải chi tiết:

Gọi H là trung điểm của BC
Tam giác ABC đều nên AH vuông góc với BC
Suy ra \(d\left( {A,\left( {SBC} \right)} \right) = AH\)
\(AH = \sqrt {A{C^2} - C{H^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = \sqrt 3 a\)
Mục 1 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, trước tiên chúng ta cần nắm vững lý thuyết cơ bản và các công thức liên quan. Giaitoan.edu.vn sẽ cung cấp cho bạn một bản tóm tắt lý thuyết ngắn gọn trước khi đi vào giải bài tập chi tiết.
Bài tập 1 thường là bài tập áp dụng trực tiếp kiến thức lý thuyết đã học. Để giải bài tập này, bạn cần:
Lời giải chi tiết bài tập 1:
(Giải thích chi tiết từng bước giải bài tập 1, kèm theo hình ảnh minh họa nếu cần)
Bài tập 2 có thể là bài tập nâng cao hơn, đòi hỏi bạn phải vận dụng kiến thức một cách linh hoạt và sáng tạo. Để giải bài tập này, bạn cần:
Lời giải chi tiết bài tập 2:
(Giải thích chi tiết từng bước giải bài tập 2, kèm theo hình ảnh minh họa nếu cần)
Bài tập 3 có thể là bài tập tổng hợp, kết hợp nhiều kiến thức khác nhau. Để giải bài tập này, bạn cần:
Lời giải chi tiết bài tập 3:
(Giải thích chi tiết từng bước giải bài tập 3, kèm theo hình ảnh minh họa nếu cần)
Bài tập 4 có thể là bài tập thực tế, ứng dụng kiến thức vào cuộc sống. Để giải bài tập này, bạn cần:
Lời giải chi tiết bài tập 4:
(Giải thích chi tiết từng bước giải bài tập 4, kèm theo hình ảnh minh họa nếu cần)
Để đạt kết quả tốt nhất khi giải bài tập Toán 11 tập 2, bạn nên:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cố gắng mang đến cho các em những trải nghiệm học tập tốt nhất, giúp các em tự tin hơn trong quá trình học tập môn Toán.
| Bài tập | Trang | Lời giải |
|---|---|---|
| Bài tập 1 | 73 | Xem lời giải |
| Bài tập 2 | 73 | Xem lời giải |
| Bài tập 3 | 74 | Xem lời giải |
| Bài tập 4 | 74 | Xem lời giải |