Bài 4.21 trang 114 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.21 trang 114 SGK Toán 11 tập 1, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:
Đề bài
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:
a) Hai mặt phẳng (BDA') và (B'D'C) song song với nhau.
b) Đường chéo AC' đi qua các trọng tâm G1 và G2 của hai tam giác BDA' và B'D'C.
c) G1 và G2 chia đoạn AC' thành ba phần bằng nhau.
Phương pháp giải - Xem chi tiết
a) Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
b) Trọng tâm là giao điểm của các đường trung tuyến.
c) Khoảng cách từ trọng tâm đến mỗi đỉnh bằng 2/3 đường trung tuyến tương ứng của đỉnh đó.
Lời giải chi tiết
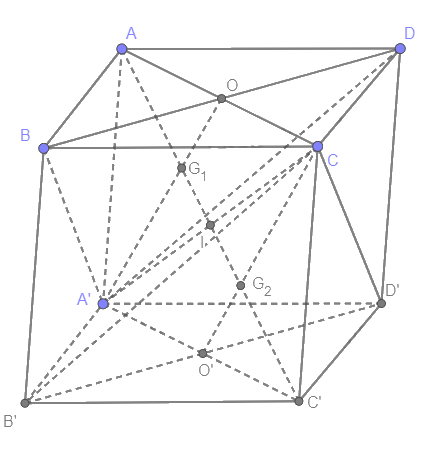
a) Ta có: BB' // DD' (cùng // CC') và BB' = DD' (cùng = CC') nên BB'D'D là hình bình hành
Suy ra BD // B'D'. Nên BD // (B'D'C) (1)
BC // A'D' (cùng // AD) và BC = A'D' (cùng = AD) nên BCD'A' là hình bình hành
Suy ra A'B // CD'. Nên A'B // (B'D'C) (2)
Từ (1) và (2) suy ra (BDA') song song với (B'D'C)
b) Gọi O, O' lần lượt là giao điểm của AC và BD, A'C' và B'D'. Suy ra O, O' là trung điểm của AC, A'C'
Gọi I là giao điểm của AC' và A'C
AA' // CC' (cùng // BB') và AA' = CC' (cùng = BB') nên ACC'A' là hình bình hành. Suy ra I là trung điểm của AC' và A'C
Nên AI và A'O là trung tuyến của tam giác AA'C
Mà G1 là trọng tâm tam giác BDA'. Suy ra G1 là giao điểm của AI và A'O
Tương tự, G2 là giao điểm của CO' và C'I
G1 thuộc AI, G2 thuộc CI nên G1 và G2 đều thuộc AC'.
c) G1 và G2 là trọng tâm của hai tam giác BDA' và B'D'C nên \(A{G_1} = \frac{2}{3}AI,{G_1}I = \frac{1}{3}AI\) và \(C'{G_2} = \frac{2}{3}C'I,{G_2}I = \frac{1}{3}CI\)
Ta có: \({G_1}I + {G_2}I = \frac{1}{3}AI + \frac{1}{3}CI = \frac{1}{3}AI + \frac{1}{3}AI = \frac{2}{3}AI\)
Suy ra AG1 = G1G2 = C'G2 (cùng = \(\frac{2}{3}AI\))
Vậy G1 và G2 chia đoạn AC' thành ba phần bằng nhau.
Bài 4.21 trang 114 SGK Toán 11 tập 1 thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản như:
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp học sinh lựa chọn phương pháp giải phù hợp và tránh sai sót trong quá trình giải.
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng và minh họa bằng hình vẽ nếu cần thiết. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm bắt được phương pháp giải bài toán.)
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ cung cấp một số ví dụ minh họa và bài tập tương tự. Các ví dụ này sẽ giúp học sinh rèn luyện kỹ năng giải toán và áp dụng kiến thức vào các bài toán khác.
Ví dụ 1: Cho hai đường thẳng d1 và d2 song song với nhau. Một mặt phẳng (P) chứa đường thẳng d1. Hỏi mặt phẳng (P) có song song với đường thẳng d2 hay không? Giải thích.
Bài tập 1: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng mặt phẳng (SMC) chứa đường thẳng song song với cạnh AD.
Kiến thức về đường thẳng và mặt phẳng có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, kỹ thuật, và đồ họa máy tính. Ví dụ, trong kiến trúc, kiến trúc sư sử dụng kiến thức này để thiết kế các công trình xây dựng có hình dạng phức tạp. Trong kỹ thuật, kỹ sư sử dụng kiến thức này để thiết kế các bộ phận máy móc và các hệ thống cơ khí.
Bài 4.21 trang 114 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Để học tốt môn Toán 11, học sinh cần nắm vững các kiến thức cơ bản, rèn luyện kỹ năng giải toán thường xuyên, và áp dụng kiến thức vào các bài toán thực tế.
giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 4.21 trang 114 SGK Toán 11 tập 1 và đạt kết quả tốt trong môn học.