Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 35, 36 SGK Toán 11 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập về nhà.
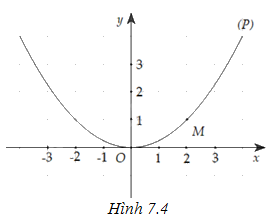
Cho hàm số \(f(x) = \frac{{{x^2}}}{4}\) có đồ thị là đường parabol (P) như Hình 7.4 . Gọi M là điểm thuộc (P) có hoành độ \({x_0} = 2\).
Cho hàm số \(f(x) = \frac{{{x^2}}}{4}\) có đồ thị là đường parabol (P) như Hình 7.4 . Gọi M là điểm thuộc (P) có hoành độ \({x_0} = 2\).
a, Tính \({f'}(2)\)
b, Viết phương trình đường thẳng \(\Delta \) đi qua điểm M và có hệ số góc bằng \({f'}(2)\)
c, Vẽ đường thẳng \(\Delta \) và (P) trên cùng một mặt phẳng tọa độ. Có nhận xét gì về \(\Delta \) và (P).
Phương pháp giải:
a, Áp dụng định nghĩa tính \({f'}(2)\)
b, Phương trình đường thẳng đi qua điểm M có hoành độ \({x_0}\) và hệ số góc \({f'}(2)\) là
\(y = {f'}({x_0}).(x - {x_0})\)
c, Dựa vào câu b để vẽ đường thẳng \(\Delta \)
Lời giải chi tiết:
a, Ta có: \({f'}(2) = \mathop {\lim }\limits_{x \to 2} \frac{{f(x) - f(2)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\frac{{{x^2}}}{4} - 1}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{4(x - 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2).(x + 2)}}{{4(x - 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{x + 2}}{4} = 1\)
b, Điểm M có tọa độ M(2;1)
Phương trình đường thẳng \(\Delta \) đi qua điểm M(2,1) có hệ số góc \({f'}(2)\) là:
y = 1.( x-2)+1= x-1
Vậy phương trình đường thẳng \(\Delta \) là: y= x-1
Cho hàm số \(y = - 3{x^3}\) có đồ thị ( C ). Tìm hệ số góc của tiếp tuyến tại điểm M (-1,3)
Phương pháp giải:
Hệ số góc của tiếp tuyến là đạo hàm của hàm số tại điểm -1
Lời giải chi tiết:
Ta có: \({f'}( - 1) = \mathop {\lim }\limits_{x \to - 1} \frac{{f(x) - f( - 1)}}{{x - ( - 1)}} = \mathop {\lim }\limits_{x \to - 1} \frac{{ - 3{x^3} - 3}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} \frac{{ - 3.({x^3} + 1)}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} ( - 3).({x^2} - x + 1) = - 9\)
Vậy hệ số góc của tiếp tuyến tại điểm M(-1,3) là -9.
Cho hàm số \(f(x) = {x^2} + 1\)có đồ thị parabol (P) và điểm M(1,2) thuộc (P). Gọi \(\Delta \)là tiếp tuyến của (P) tại M. Hãy viết phương trình \(\Delta \).
Phương pháp giải:
Hệ số góc của tiếp tuyến là đạo hàm của hàm số tại điểm 1
Phương trình tiếp tuyến của đường thẳng có hệ số góc k tại điểm \(M({x_0};{y_0})\) là:
\(y = k.(x - {x_0}) + {y_0}\)
Lời giải chi tiết:
Ta có: \(y'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + 1 - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x + 1) = 2\)
Phương trình tiếp tuyến tại điểm M(1,2) có hệ số góc k=2 là:
y = 2.( x -1)+2=2x
Cho parabol (P) \(y = {x^2} + 2x - 3\) và điểm M thuộc (P) có hoành độ \({x_0} = - 2\)
a, Tính \({y'}( - 2)\)
b, Viết phương trình tiếp tuyến của (P) tại điểm M.
Phương pháp giải:
a, Sử dụng định nghĩa để tìm đạo hàm của hàm số tại điểm -2
b, Sử dụng công thức tiếp tuyến \(y = {f'}({x_0}).(x - {x_0}) + f({x_0})\)
Lời giải chi tiết:
a, Ta có: \(y'( - 2) = \mathop {\lim }\limits_{x \to - 2} \frac{{f(x) - f( - 2)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} + 2x - 3 - ( - 3)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} + 2x}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{x.(x + 2)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} x = - 2\)
b, Ta có: \({x_0} = - 2 \Rightarrow f({x_0}) = {( - 2)^2} + 2.( - 2) - 3 = - 3\)
Phương trình tiếp tuyến của (P) tại điểm M (-2, -3) là:
y = -2. (x + 2) -3= -2x -7.
Mục 2 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề là yếu tố then chốt để tìm ra lời giải chính xác.
Để cung cấp một giải pháp toàn diện, chúng ta cần xem xét từng bài tập cụ thể trong mục 2 trang 35, 36. Dưới đây là phân tích chi tiết và lời giải cho từng bài:
Đề bài: (Nêu rõ đề bài của bài tập)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và định lý liên quan. Có thể sử dụng hình ảnh minh họa nếu cần thiết.)
Đề bài: (Nêu rõ đề bài của bài tập)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và định lý liên quan. Có thể sử dụng hình ảnh minh họa nếu cần thiết.)
Đề bài: (Nêu rõ đề bài của bài tập)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và định lý liên quan. Có thể sử dụng hình ảnh minh họa nếu cần thiết.)
Để giải quyết hiệu quả các bài tập trong mục 2, học sinh có thể áp dụng các phương pháp sau:
Trong mục 2, học sinh có thể gặp các dạng bài tập sau:
Khi giải bài tập Toán 11 tập 2, học sinh cần lưu ý những điều sau:
Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 35, 36 SGK Toán 11 tập 2. Chúc các em học tập tốt!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Tóm tắt lời giải bài 1) |
| Bài 2 | (Tóm tắt lời giải bài 2) |
| Bài 3 | (Tóm tắt lời giải bài 3) |