Chào mừng bạn đến với bài giải Bài 5.12 trang 145 SGK Toán 11 tập 1 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ bạn học Toán 11 hiệu quả nhất. Hãy cùng khám phá!
Điều tra quãng đường mà mỗi xe buýt các tuyến nội thành thực hiện vào một ngày làm việc bình thường trong tuần, Trung tâm Quảng lí giao thông công cộng lập được Bảng 5.32:
Đề bài
Điều tra quãng đường mà mỗi xe buýt các tuyến nội thành thực hiện vào một ngày làm việc bình thường trong tuần, Trung tâm Quảng lí giao thông công cộng lập được Bảng 5.32:
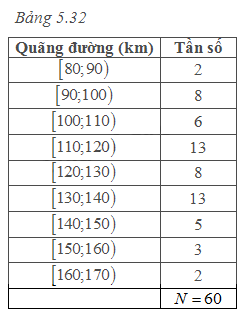
Nam và Lan cùng phân tích bảng dữ liệu để tìm quãng đường đi phổ biến của các xe buýt. Theo Nam, quãng đường xấp xỉ 116 km là quãng đường được nhiều xe thực hiện nhất. Lan không đồng ý, cho rằng quãng đường dài xấp xỉ 134 km mới là quãng đường được nhiều xe thực hiện nhất. Có hay không điểm bất hợp lí trong ý kiến của mỗi bạn Nam, Lan? Giải thích vì sao.
Phương pháp giải - Xem chi tiết
Có hai nhóm có cùng tần số, vậy mẫu số liệu có 2 mốt. Ta đi tính hai mốt đó
Nhóm chứa mốt là nhóm mà có tần số nhiều nhất
Mốt của mẫu số liệu ghép nhóm được tính theo công thức: \({M_0} = {L_m} + \frac{a}{{a + b}}.h\)
Trong đó:
\({L_m}\) là đầu mút trái của nhóm chứa mốt;
\(h\) là độ dài của nhóm chứa mốt;
\(a = {n_0} - {n_1};b = {n_0} - {n_2}\) với \({n_0};{n_1};{n_2}\) tương ứng là tần số của nhóm chứa mốt, nhóm liền kề trước và nhóm liền kề sau nhóm chứa mốt.
Lời giải chi tiết
Ta thấy mẫu số liệu có hai nhóm \(\left[ {110;120} \right)\) và \(\left[ {130;140} \right)\) có cùng tần số là 13 và là tần số cao nhất. Do đó, bài toán có 2 mốt.
+) Với nhóm chứa mốt \(\left[ {110;120} \right)\) có tần số 13. Do đó \({L_m} = 110;h = 120 - 110 = 10\)
\(a = 13 - 6 = 7;b = 13 - 8 = 5\). Khi đó \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 110 + \frac{7}{{7 + 5}}.10 \approx 116\)
Do đó, quãng đường xấp xỉ 116 km là quãng đường được nhiều xe thực hiện nhất.
+) Với nhóm chứa mốt \(\left[ {130;140} \right)\) có tần số 13. Do đó \({L_m} = 130;h = 140 - 130 = 10\)
\(a = 13 - 8 = 5;b = 13 - 5 = 8\). Khi đó \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 130 + \frac{5}{{5 + 8}}.10 \approx 134\)
Do đó, quãng đường xấp xỉ 134 km là quãng đường được nhiều xe thực hiện nhất.
Từ hai kết quả trên ta thấy cả hai ý kiến của mỗi bạn Nam, Lan đều hợp lí.
Bài 5.12 trang 145 SGK Toán 11 tập 1 thuộc chương trình học về hàm số lượng giác. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác, các công thức lượng giác cơ bản và các tính chất của hàm số lượng giác để giải quyết.
Thông thường, bài tập 5.12 sẽ yêu cầu:
Để giải quyết bài tập này một cách hiệu quả, bạn cần:
Bài tập: Tìm tập xác định của hàm số y = tan(2x + π/3).
Giải:
Hàm số y = tan(2x + π/3) xác định khi và chỉ khi cos(2x + π/3) ≠ 0.
Điều này tương đương với 2x + π/3 ≠ π/2 + kπ, với k là số nguyên.
Suy ra 2x ≠ π/2 - π/3 + kπ = π/6 + kπ.
Vậy x ≠ π/12 + kπ/2, với k là số nguyên.
Kết luận: Tập xác định của hàm số là D = R \ {π/12 + kπ/2, k ∈ Z}.
Ngoài việc tìm tập xác định, bài tập 5.12 còn có thể xuất hiện các dạng bài sau:
Để đạt kết quả tốt nhất, bạn nên:
Ngoài SGK Toán 11 tập 1, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Bài 5.12 trang 145 SGK Toán 11 tập 1 và tự tin giải quyết các bài tập tương tự. Chúc bạn học tập tốt!