Bài 5.9 trang 141 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải nhanh chóng cho Bài 5.9 trang 141 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
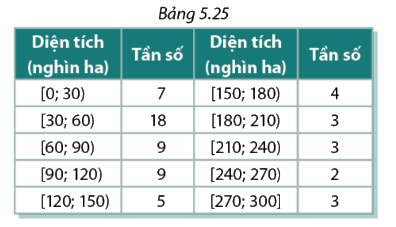
Tham khảo trang https:///www.gso.gov.vn/ Mai thống kê diện tích trồng lúa năm 2019 của 63 tỉnh thành và tổ chức dữ liệu trong Bảng 5.25
Đề bài
Tham khảo trang https:///www.gso.gov.vn/Mai thống kê diện tích trồng lúa năm 2019 của 63 tỉnh thành và tổ chức dữ liệu trong Bảng 5.25
a, Xác định các tứ phân vị của mẫu số liệu
b, Kết quả tìm được cho biết thông tin gì về diện tích trồng lúa năm 2019
Phương pháp giải - Xem chi tiết
a, Sử dụng công thức tính tứ phân vị của mẫu số liệu
b, Dựa vào kết quả câu a để làm câu b
Lời giải chi tiết
a, Bảng tần số tích lũy của mẫu số liệu
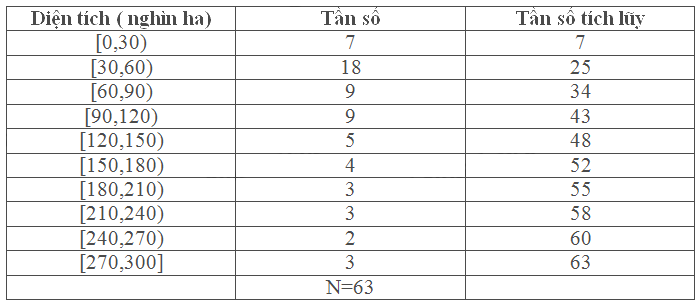
Ta có: \(\frac{N}{4} = \frac{{63}}{4} \Rightarrow \frac{N}{2} = \frac{{63}}{2} \Rightarrow \frac{{3N}}{4} = \frac{{189}}{4}\)
Các nhóm chứa \({Q_1}\), \({Q_2}\) và \({Q_3}\) là [30,60); [60,90) và [120,150)
Độ dài các nhóm ghép đều là h= 30
Ta có: \({L_1} = 30,{n_1} = 18,{T_1} = 7\)\( \Rightarrow {Q_1} = {L_1} + \frac{{\frac{N}{4} - {T_1}}}{{{n_1}}}.h = 30 + \frac{{\frac{{63}}{4} - 7}}{{18}}.30 \approx 44,58\)
\({L_2} = 60,{n_2} = 9,{T_2} = 25\)\( \Rightarrow {Q_2} = {L_2} + \frac{{\frac{N}{2} - {T_2}}}{{{n_2}}}.h = 60 + \frac{{\frac{{63}}{2} - 25}}{9}.30 \approx 81,67\)
\({L_3} = 120,{n_3} = 5,{T_3} = 43\)\( \Rightarrow {Q_3} = {L_3} + \frac{{\frac{{3N}}{4} - {T_3}}}{{{n_3}}}.h = 120 + \frac{{\frac{{189}}{4} - 43}}{5}.30 = 145,5\)
Vậy làm tròn số ta được \({Q_1}\)=45, \({Q_2}\)=82 và \({Q_3}\)=146.
b, Theo kết quả câu a, ta có:
Có ít nhất 25 % số tỉnh có diện tích không vượt quá 45 nghìn ha. Cúng như vậy khoảng 50 % số tỉnh có diện tích không vượt quá 82 nghìn ha, khoảng 75 % số tỉnh có diện tích không vượt quá 146 nghìn ha và khoảng 25% số tỉnh có diện tích từ 45 nghìn ha trở lên.
Đối với 50 % số tỉnh có diện tích ở trung tâm của dữ liệu thì đầu mút trái của khoảng điểm là 45 và đầu mút phải của khoảng điểm là 146. Vậy số tuổi của lao động tập trung ở [45,82]
Bài 5.9 trang 141 SGK Toán 11 tập 1 thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập:
Bài 5.9 yêu cầu tính đạo hàm của hàm số tại một điểm cho trước hoặc tìm đạo hàm của hàm số. Thông thường, bài tập sẽ cho một hàm số cụ thể và yêu cầu tính đạo hàm f'(x) hoặc f'(x0).
Phương pháp giải:
Ví dụ minh họa:
Giả sử hàm số f(x) = x2 + 2x + 1. Để tính đạo hàm f'(x), ta áp dụng quy tắc đạo hàm của tổng và đạo hàm của hàm số đa thức:
f'(x) = (x2)' + (2x)' + (1)' = 2x + 2 + 0 = 2x + 2
Các dạng bài tập thường gặp:
Lưu ý khi giải bài tập:
Mở rộng kiến thức:
Ngoài việc giải Bài 5.9 trang 141 SGK Toán 11 tập 1, các em học sinh nên tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, như việc tìm cực trị của hàm số, giải các bài toán tối ưu hóa, và nghiên cứu sự biến thiên của hàm số.
Tài liệu tham khảo:
Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng này, các em học sinh sẽ tự tin hơn khi giải Bài 5.9 trang 141 SGK Toán 11 tập 1 và các bài tập tương tự. Chúc các em học tốt!