Bài 5.4 trang 133 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc giải các phương trình lượng giác cơ bản. Bài tập này giúp học sinh rèn luyện kỹ năng biến đổi lượng giác và áp dụng các công thức lượng giác đã học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 5.4 trang 133, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bảng 5.13 trình bày dữ liệu liên quan của 160 chuyến xe mà một tài xế đã hoàn thành trong một tháng.
Đề bài
Bảng 5.13 trình bày dữ liệu liên quan của 160 chuyến xe mà một tài xế đã hoàn thành trong một tháng. Xác định quãng đường trung bình của các chuyến xe mà tài xế này đã thực hiện trong tháng đó.

Phương pháp giải - Xem chi tiết
Lập bảng mẫu số liệu ghép nhóm để tính quãng đường trung bình
Lời giải chi tiết
Bảng mẫu số liệu ghép nhóm
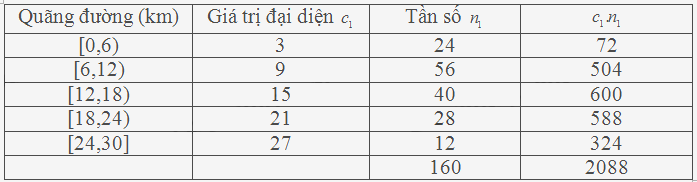
Quãng đường trung bình mà tài xế này thực hiện là:
\(\mathop x\limits^\_ = \frac{{2088}}{{160}} = 13,05\) (km)
Bài 5.4 trang 133 SGK Toán 11 tập 1 yêu cầu giải các phương trình lượng giác sau:
Phương trình tương đương với:
Phương trình tương đương với:
Phương trình tương đương với:
Phương trình tương đương với:
Để giải các phương trình lượng giác, cần nắm vững các kiến thức sau:
Khi giải phương trình lượng giác, cần chú ý đến điều kiện xác định của hàm số lượng giác. Ví dụ, hàm tan(x) xác định khi cos(x) ≠ 0, hàm cot(x) xác định khi sin(x) ≠ 0.
Để củng cố kiến thức về phương trình lượng giác, bạn có thể luyện tập thêm các bài tập sau:
Giaitoan.edu.vn cung cấp đầy đủ các bài giải chi tiết và phương pháp giải các bài tập Toán 11, giúp bạn học Toán hiệu quả và đạt kết quả cao.
Việc nắm vững kiến thức về phương trình lượng giác là rất quan trọng, không chỉ cho kỳ thi THPT Quốc gia mà còn là nền tảng cho các kiến thức Toán học nâng cao hơn. Hãy dành thời gian luyện tập và tìm hiểu kỹ các kiến thức này để đạt được kết quả tốt nhất.