Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Mục 1 trang 14, 15 SGK Toán 11 tập 2 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm và định lý liên quan.
Chúng tôi hiểu rằng việc tự giải bài tập có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải chi tiết, giúp bạn hiểu rõ từng bước giải và áp dụng vào các bài tập tương tự.
Cho biểu thức \(y = {2^x}\), trong đó x là một số thực lấy giá trị tùy ý.
Cho biểu thức \(y = {2^x}\), trong đó x là một số thực lấy giá trị tùy ý.
a) Hãy tính giá trị của y tương ứng với mỗi giá trị của x được cho trong bảng sau:
b) Với mỗi giá trị của x, ta tính được bao nhiêu giá trị của y? y có phải là hàm số của x không? Vì sao?
c) Biểu thức \(y = {\left( { - 3} \right)^x}\) có xác định một hàm số khi x lấy giá trị trong tập số thực \(\mathbb{R}\) không? Vì sao?
Phương pháp giải:
a) Thay x = 3; 0,5; \( - \frac{3}{7}\); \(\sqrt 2 \); \( - \sqrt 3 \) vào biểu thức \(y = {2^x}\).
b) Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
c) Khi số mũ nằm trong khoảng (0;1) thì cơ số không thể âm.
Lời giải chi tiết:
a)
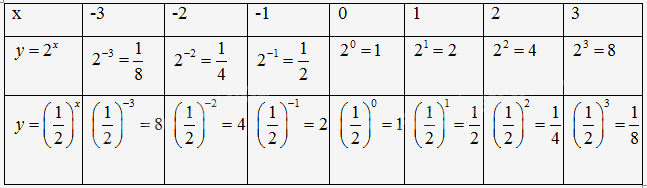
b) Với mỗi giá trị của x chỉ tính được một giá trị của y. y là hàm số của x vì mỗi một giá trị của x thì ta luôn xác định được chỉ một giá trị tương ứng của y.
c) Biểu thức \(y = {\left( { - 3} \right)^x}\) không xác định một hàm số khi x lấy giá trị trong tập số thực \(\mathbb{R}\). Vì khi \(x = \frac{1}{2}\), ta có: \({\left( { - 3} \right)^{\frac{1}{2}}} = \sqrt { - 3} \) (Vô lí)
Trong các hàm số sau, hàm số nào là hàm số mũ, với cơ số bao nhiêu? Vì sao?
a) \(y = {3^{2x}}\)
b) \(y = {\left( { - \pi } \right)^x}\)
c) \(y = {x^{ - 4}}\)
d) \(y = {4^{ - x}}\)
Phương pháp giải:
Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a với a là một số thực dương khác 1.
Lời giải chi tiết:
a) \(y = {3^{2x}}\) là hàm số mũ với cơ số bằng 3.
b) \(y = {\left( { - \pi } \right)^x}\) là hàm số mũ với cơ số bằng \(\pi \).
c) \(y = {x^{ - 4}}\) không là hàm số mũ vì cơ số không phải hằng số.
d) \(y = {4^{ - x}}\) là hàm số mũ với cơ số bằng 4.
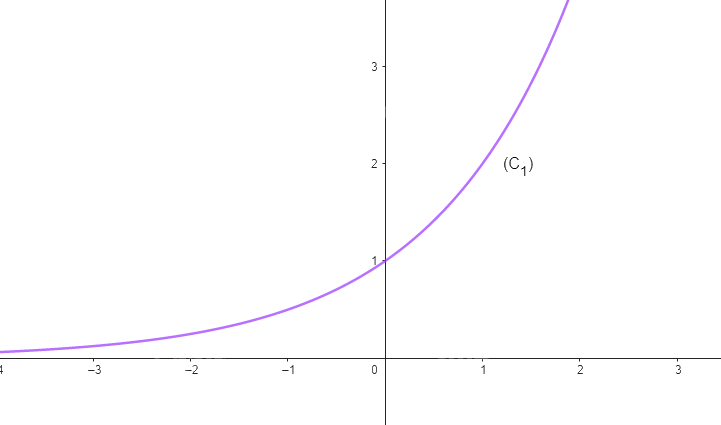
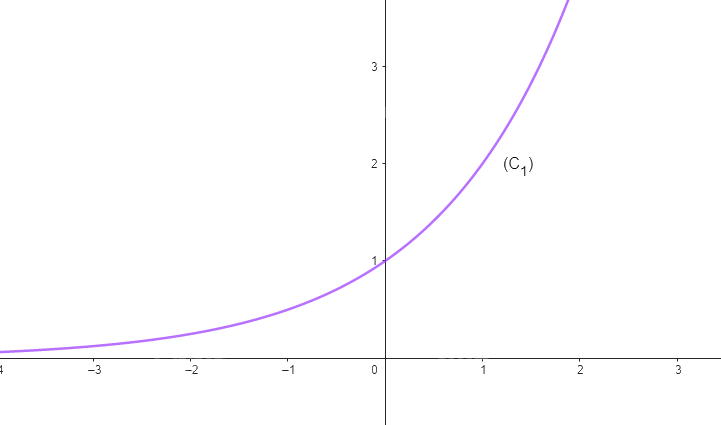
Cho hàm số \(y = {2^x}\) có đồ thị là (C1) và hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) có đồ thị (C2).
a) Hoàn thành bảng giá trị sau và biểu diễn trong mặt phẳng Oxy:

b) Vẽ đường cong nối các điểm thuộc (C1) (Theo thứ tự hoành độ tăng dần) và một đường cong khác nối các điểm thuộc (C2) (Theo thứ tự hoành độ tăng dần).
Phương pháp giải:
Thay x = -3, -2,… , 3 vào \(y = {2^x}\) và \(y = {\left( {\frac{1}{2}} \right)^x}\)
Lời giải chi tiết:
a,
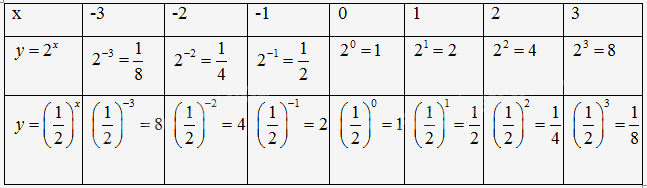
b)
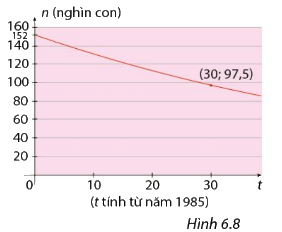
Đồ thị Hình 6.8 cho thấy số lượng hươu cao cổ trên thế giới suy giảm nghiêm trọng trong 30 năm qua (từ năm 1985 đến 2015) (nguồn: https://tuoitre.vn/huou-cao-co-sap-vao-danh-sach-loai-gap-nguy-hiem-20190428162017473.htm). Giả sử rằng số lượng hươu ở đây giảm theo hàm số \(n\left( t \right) = C.{a^t}\).
a) Tìm số lượng hươu vào năm 1985.
b) Tìm hàm số biểu diễn số lượng hươu sau t năm kể từ năm 1985.
c) Dự đoán số lượng hươu vào năm 2025.

Phương pháp giải:
a) Năm 1985 là t = 0, quan sát đồ thị khi t = 0 thì n bằng bao nhiêu.
b) Số lượng hươu mỗi năm là số lượng hươu năm 1985 trừ đi số lượng hươu giảm được tính theo hàm số \(n\left( t \right) = C.{a^t}\).
c) Kể từ năm 1985 đến 2025 là 40 năm nên t = 40. Thay t = 40 vào hàm số ở phần b.
Lời giải chi tiết:
a) Số lượng hươu năm 1985 là 152 nghìn con.
b) Ta có: \(C.{a^0} = n\left( 0 \right) \Leftrightarrow C = 152\)
\(\begin{array}{l}C.{a^{30}} = n\left( {30} \right)\\ \Leftrightarrow 152.{a^{30}} = 97,5\\ \Leftrightarrow {a^{30}} = \frac{{195}}{{304}}\\ \Leftrightarrow a = \sqrt[{30}]{{\frac{{195}}{{304}}}}\end{array}\)
\( \Rightarrow n\left( t \right) = 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^t}\)
Hàm số biểu diễn lượng hươu sau t năm kể từ năm 1985 là: \(H\left( t \right) = 152 - 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^t}\)
c) Kể từ năm 1985 đến 2025 là 40 năm nên t = 40
Số lượng hươu vào năm 2025 là: \(H\left( {40} \right) = 152 - 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^{40}} \approx 67,914\) (nghìn con)
Mục 1 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể, ví dụ như dãy số, cấp số cộng, cấp số nhân, hoặc giới hạn của dãy số. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để giải quyết các bài tập trong mục này.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại các khái niệm và định lý quan trọng liên quan đến chủ đề của Mục 1. Ví dụ, nếu Mục 1 nói về dãy số, bạn cần hiểu rõ:
Tùy thuộc vào từng dạng bài tập cụ thể, chúng ta có thể áp dụng các phương pháp giải khác nhau. Dưới đây là một số phương pháp thường được sử dụng:
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1 trang 14, 15 SGK Toán 11 tập 2. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu, kèm theo các chú thích và giải thích cần thiết.
Đề bài: (Giả định đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập)
Sau khi đã xem lời giải chi tiết, bạn nên tự mình luyện tập thêm các bài tập tương tự để củng cố kiến thức và rèn luyện kỹ năng giải toán. Bạn có thể tìm thấy thêm các bài tập trong sách bài tập, đề thi thử, hoặc trên các trang web học toán online.
Đề bài: (Giả định đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập)
Chúc bạn học tốt môn Toán 11!