Bài 4.10 trang 100 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải nhanh chóng cho bài 4.10 trang 100 SGK Toán 11 tập 1, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
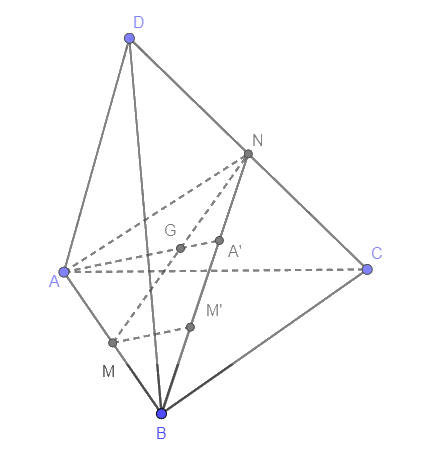
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
Đề bài
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
a) Tìm giao điểm A' của đường thẳng AG và mặt phẳng (BCD).
b) Qua M, kẻ đường thẳng Mx song song với AA' và Mx cắt (BCD) tại M'. Chứng minh B, M', A' thẳng hằng và BM'=M'A'=A'N.
Phương pháp giải - Xem chi tiết
a) Cách tìm giao điểm của một đường thẳng a với một mặt phẳng (P):
+ Bước 1: Tìm \(\left( Q \right) \supset a\). Tìm \(d = \left( P \right) \cap \left( Q \right)\)
+ Bước 2: Tìm \(I = a \cap d\). I chính là giao điểm của a và (P).
b) Chứng minh 3 điểm cùng thuộc 2 mặt phẳng phân biệt thì 3 điểm đó thẳng hàng.
Lời giải chi tiết
a)
\(\left\{ \begin{array}{l}G \in MN\\MN \subset \left( {ABN} \right)\end{array} \right. \Rightarrow G \in \left( {ABN} \right)\)
\( \Rightarrow AG \subset \left( {ABN} \right)\)
Ta có: \(\left( {ABN} \right) \cap \left( {BCD} \right) = BN\)
Trong (ABN), gọi \(AG \cap BN = A'\) \( \Rightarrow A' = AG \cap \left( {BCD} \right)\)
b)
\(\left\{ \begin{array}{l}Mx//AA'\\AA' \subset \left( {ABN} \right)\\M \in \left( {ABN} \right)\end{array} \right. \Rightarrow Mx \subset \left( {ABN} \right)\)
Mà \(M' = Mx \cap \left( {BCD} \right)\)
Suy ra \({{\rm{M}}^{\rm{'}}}\) nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.
Vậy B, M’, A’ thẳng hàng.
Xét tam giác \(ABA'\) có: \(\left\{ \begin{array}{l}MM'//AA'\\MA = MB\end{array} \right. \Rightarrow M'A' = M'B\)
Xét tam giác \(NMM'\) có: \(\left\{ \begin{array}{l}GA//MM'\\MG = GN\end{array} \right. \Rightarrow M'A' = A'N\)
\( \Rightarrow BM' = M'A' = A'N\).
Bài 4.10 trang 100 SGK Toán 11 tập 1 thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản như:
Nội dung bài tập:
Bài 4.10 yêu cầu học sinh chứng minh một số tính chất liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng, hoặc xác định giao điểm của đường thẳng và mặt phẳng. Cụ thể, bài tập có thể yêu cầu:
Lời giải chi tiết:
Để giải bài 4.10 trang 100 SGK Toán 11 tập 1, chúng ta cần thực hiện các bước sau:
Ví dụ minh họa:
Giả sử bài tập yêu cầu chứng minh đường thẳng d song song với mặt phẳng (P). Ta có thể thực hiện như sau:
1. Tìm một điểm A thuộc đường thẳng d.
2. Chứng minh rằng đường thẳng d không nằm trong mặt phẳng (P).
3. Chứng minh rằng đường thẳng d và mặt phẳng (P) không có điểm chung.
Nếu chứng minh được cả ba điều kiện trên, ta có thể kết luận rằng đường thẳng d song song với mặt phẳng (P).
Mở rộng kiến thức:
Ngoài bài 4.10 trang 100 SGK Toán 11 tập 1, học sinh có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập về đường thẳng và mặt phẳng trong không gian.
Lưu ý:
Khi giải bài tập về đường thẳng và mặt phẳng trong không gian, học sinh cần chú ý đến việc vẽ hình chính xác và sử dụng các ký hiệu toán học một cách đúng đắn. Ngoài ra, việc hiểu rõ các định nghĩa và tính chất cơ bản cũng rất quan trọng để giải quyết các bài toán một cách hiệu quả.
Các bài tập liên quan:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải bài 4.10 trang 100 SGK Toán 11 tập 1. Chúc các em học tập tốt!