Bài 5.21 thuộc chương trình Toán 11 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng tính đạo hàm của hàm số.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Dưới đây là một mẫu số liệu cho ở dạng bảng tần số ghép nhóm:
Đề bài
Dưới đây là một mẫu số liệu cho ở dạng bảng tần số ghép nhóm:

Trung bình của mẫu số liệu ghép nhóm là
A. \(\overline x \approx 112,8.\)
B. \(\overline x \approx 107,8.\)
C. \(\overline x \approx 102,5.\)
D. \(\overline x \approx 85,5.\)
Phương pháp giải - Xem chi tiết
+) \(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
Lời giải chi tiết
Để ngắn gọn, ta lập bảng sau
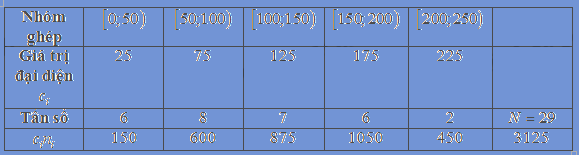
Áp dụng công thức tính trung bình ta có \(\overline x = \frac{{3125}}{{29}} \approx 107,8\)
Đáp án B
Bài 5.21 SGK Toán 11 tập 1 yêu cầu học sinh giải một bài toán liên quan đến đạo hàm của hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Phân tích bài toán:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và các dữ kiện đã cho. Sau đó, chúng ta cần phân tích bài toán để tìm ra phương pháp giải phù hợp.
Lời giải chi tiết:
Để giải bài 5.21 trang 149 SGK Toán 11 tập 1, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa:
Giả sử bài toán yêu cầu tìm cực trị của hàm số y = x3 - 3x2 + 2.
Bước 1: Tính đạo hàm:
y' = 3x2 - 6x
Bước 2: Giải phương trình đạo hàm:
3x2 - 6x = 0
3x(x - 2) = 0
x = 0 hoặc x = 2
Bước 3: Xác định loại điểm cực trị:
y'' = 6x - 6
Tại x = 0, y'' = -6 < 0, vậy x = 0 là điểm cực đại.
Tại x = 2, y'' = 6 > 0, vậy x = 2 là điểm cực tiểu.
Bước 4: Tính giá trị của hàm số tại các điểm cực trị:
Tại x = 0, y = 2.
Tại x = 2, y = 0.
Vậy hàm số đạt cực đại tại điểm (0, 2) và đạt cực tiểu tại điểm (2, 0).
Lưu ý:
Trong quá trình giải bài toán, chúng ta cần chú ý đến các điều kiện của bài toán và kiểm tra lại kết quả để đảm bảo tính chính xác.
Ứng dụng của đạo hàm:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài tập tương tự:
Để củng cố kiến thức về đạo hàm, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 11 tập 1 và các tài liệu tham khảo khác.
Kết luận:
Bài 5.21 trang 149 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các bạn học sinh có thể tự tin giải bài tập này và các bài tập tương tự.