Bài 5.15 trang 147 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải nhanh chóng cho bài tập này, giúp học sinh nắm vững kiến thức và tự tin làm bài.
Một du học sinh ở nước ngoài đã tìm hiểu mức lương của nhận viên thuộc một công ty và thu được Bảng 5.35 dưới đây. Nếu xét về lương thì có hay không sự bất bình đẳng giữa nam giới và nữ giới làm việc ở công ty này? Giải thích câu trả lời bằng cách dựa vào các tham số đo xu thế trung tâm (trung bình, trung vị, mốt) của mẫu số liệu.
Đề bài
Một du học sinh ở nước ngoài đã tìm hiểu mức lương của nhận viên thuộc một công ty và thu được Bảng 5.35 dưới đây. Nếu xét về lương thì có hay không sự bất bình đẳng giữa nam giới và nữ giới làm việc ở công ty này? Giải thích câu trả lời bằng cách dựa vào các tham số đo xu thế trung tâm (trung bình, trung vị, mốt) của mẫu số liệu.

Phương pháp giải - Xem chi tiết
+) \(\overline x \) của mẫu số liệu ghép nhóm được tính theo công thức
\(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
+) Trung vị \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\) trong đó \({L_m},{n_m},h\) lần lượt là đầu mút trái, tần số và độ dài của nhóm chứa trung vị. \(T\) là tần số tích lũy của nhóm ngay trước nhóm chứa trung vị.
Nhóm chứa trung vị của mẫu số liệu là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\) , trong đó \(N\) là cỡ mẫu.
+) Công thức tìm mốt của mẫu số liệu ghép nhóm là \({M_0} = {L_m} + \frac{a}{{a + b}}.h\)
Lời giải chi tiết
+) Tính trung bình
Để ngắn gọn, ta lập bảng sau
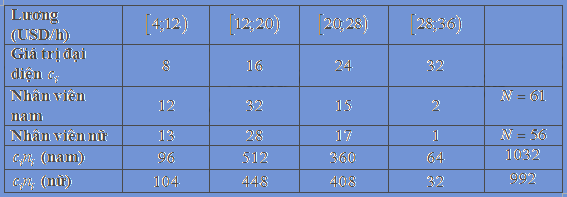
Ta có lương trung bình của nam là \(\overline x = \frac{{1032}}{{61}} \approx 16,9\) USD
Lương trung bình của nữ là \(\overline x = \frac{{992}}{{59}} \approx 16,8\) USD
+) Tìm trung vị
Để ngắn gọn, ta lập bảng sau
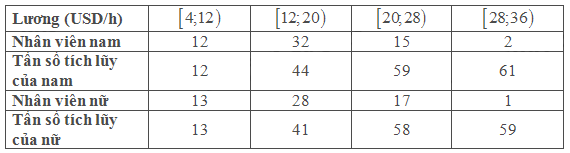
Đối với nam thì \(\frac{N}{2} = \frac{{61}}{2} = 30,5\). Nhóm đầu tiên có tần số tích lũy lớn hơn bằng \(30,5\) là nhóm \(\left[ {12;20} \right)\) và đây là nhóm chứa trung bị với \({L_m} = 12,\) tần số \({n_m} = 32\), \(h = 20 - 12 = 8\), tần số tích lũy của nhóm trước nhóm chứa trung vị là \(T = 12\)
Áp dụng công thức tính trung vị ta có \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 12 + \frac{{30,5 - 12}}{{32}}.8 \approx 16,6\)
Đối với nữa thì \(\frac{N}{2} = \frac{{59}}{2} = 29,5\). Nhóm đầu tiên có tần số tích lũy lớn hơn bằng \(29,5\) là nhóm \(\left[ {12;20} \right)\) và đây là nhóm chứa trung bị với \({L_m} = 12,\) tần số \({n_m} = 28\), \(h = 20 - 12 = 8\), tần số tích lũy của nhóm trước nhóm chứa trung vị là \(T = 13\)
Áp dụng công thức tính trung vị ta có \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 12 + \frac{{29,5 - 13}}{{28}}.8 \approx 16,7\)
+) Tìm mốt
Đối với nam thì nhóm chứa mốt là \(\left[ {12;20} \right)\) với \({L_m} = 12;h = 20 - 12 = 8\)
\(a = 32 - 12 = 20,b = 32 - 15 = 17\)
Áp dụng công thức tính mốt ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 12 + \frac{{20}}{{20 + 17}}.8 \approx 16,3\)
Đối với nam thì nhóm chứa mốt là \(\left[ {12;20} \right)\) với \({L_m} = 12;h = 20 - 12 = 8\)
\(a = 28 - 13 = 15,b = 28 - 17 = 11\)
Áp dụng công thức tính mốt ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 12 + \frac{{15}}{{15 + 11}}.8 \approx 16,6\)
Dựa vào các tham số đo xu thế trung tâm ta nhận thấy xét về lương thì không có sự bất bình đẳng giữa nam giới và nữ giới.
Bài 5.15 trang 147 SGK Toán 11 tập 1 thuộc chương trình Đại số, cụ thể là phần Đạo hàm. Bài toán này thường yêu cầu học sinh áp dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác.
Để giải quyết bài toán này, trước hết, chúng ta cần xác định rõ yêu cầu của đề bài. Thông thường, bài toán sẽ yêu cầu tính đạo hàm của một hàm số cho trước tại một điểm cụ thể hoặc tìm điều kiện để hàm số có đạo hàm. Việc hiểu rõ yêu cầu là bước đầu tiên quan trọng để tìm ra phương pháp giải phù hợp.
Giả sử bài toán yêu cầu tính đạo hàm của hàm số f(x) = sin(2x) tại điểm x = π/4. Chúng ta sẽ thực hiện như sau:
Vậy, đạo hàm của hàm số f(x) = sin(2x) tại điểm x = π/4 là 0.
Ngoài việc tính đạo hàm trực tiếp, bài toán còn có thể yêu cầu:
Khi giải bài tập về đạo hàm, cần lưu ý những điều sau:
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin giải quyết Bài 5.15 trang 147 SGK Toán 11 tập 1 một cách hiệu quả. Chúc bạn học tập tốt!