Bài 5.8 trang 141 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải nhanh chóng cho Bài 5.8 trang 141 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
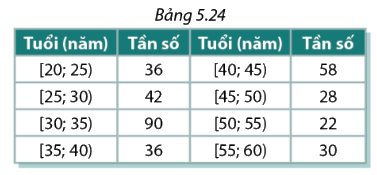
Tuổi của một số lao động nam được thống kê trong Bảng 5.24
Đề bài
Tuổi của một số lao động nam được thống kê trong Bảng 5.24
a, Xác định các tứ phân vị của mẫu số liệu
b, Kết quả tìm được cho biết thông tin gì về độ tuổi của các lao động nam được điều tra
Phương pháp giải - Xem chi tiết
a, Từ công thức xác định các tứ phân vị
b, Từ kết quả câu a xác định câu b
Lời giải chi tiết
a, Bảng tần số tích lũy của mẫu số liệu
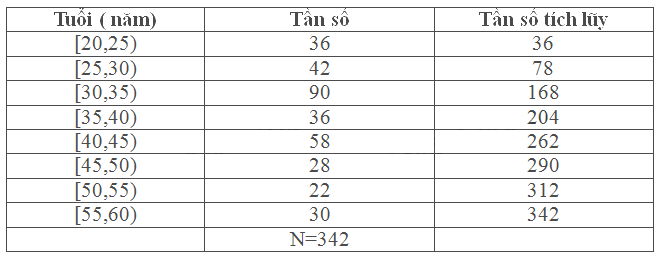
Ta có: \(\frac{N}{4} = \frac{{342}}{4} = 85,5 \Rightarrow \frac{N}{2} = 171 \Rightarrow \frac{{3N}}{4} = 256,5\)
Các nhóm chứa \({Q_1}\), \({Q_2}\) và \({Q_3}\) là [30,35); [35,40) và [40,45)
Độ dài các nhóm ghép đều là h= 5
Ta có: \({L_1} = 30,{n_1} = 90,{T_1} = 78\)\( \Rightarrow {Q_1} = {L_1} + \frac{{\frac{N}{4} - {T_1}}}{{{n_1}}}.h = 30 + \frac{{85,5 - 78}}{{90}}.5 \approx 30,42\)
\({L_2} = 35,{n_2} = 36,{T_2} = 168\)\( \Rightarrow {Q_2} = {L_2} + \frac{{\frac{N}{2} - {T_2}}}{{{n_2}}}.h = 35 + \frac{{171 - 168}}{{36}}.5 \approx 35,42\)
\({L_3} = 40,{n_3} = 58,{T_3} = 204\)\( \Rightarrow {Q_3} = {L_3} + \frac{{\frac{{3N}}{4} - {T_3}}}{{{n_3}}}.h = 40 + \frac{{256,5 - 204}}{{58}}.5 \approx 44,53\)
Như vậy làm tròn kết quả ta có: \({Q_1}\)=30, \({Q_2}\)=35 và \({Q_3}\)=45
b, Theo kết quả câu a, ta có:
Có ít nhất 25 % lao động nam có số tuổi không vượt quá 30. Cúng như vậy khoảng 50 % lao động nam có số tuổi không vượt quá 35, khoảng 75 % lao động nam có số tuổi không vượt quá 45 và khoảng 25% lao động nam có số tuổi từ 45 trở lên.
Đối với 50 % lao động nam có số tuổi ở trung tâm của dữ liệu thì đầu mút trái của khoảng điểm là 30 và đầu mút phải của khoảng điểm là 45. Vậy số tuổi của lao động tập trung ở [30,35]
Bài 5.8 trang 141 SGK Toán 11 tập 1 thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập:
Bài 5.8 yêu cầu tính đạo hàm của các hàm số được cho. Ví dụ, một hàm số có thể là f(x) = x3 + 2x2 - 5x + 1. Để tính đạo hàm của hàm số này, ta áp dụng quy tắc đạo hàm của tổng và quy tắc đạo hàm của hàm số đa thức.
Lời giải chi tiết:
f'(x) = (x3)' + (2x2)' - (5x)' + (1)'
f'(x) = 3x2 + 4x - 5 + 0
f'(x) = 3x2 + 4x - 5
Phương pháp giải:
Để giải các bài tập về đạo hàm, học sinh nên thực hiện theo các bước sau:
Ví dụ minh họa:
Xét hàm số g(x) = sin(x) + cos(x). Để tính đạo hàm của hàm số này, ta áp dụng quy tắc đạo hàm của tổng và đạo hàm của các hàm số lượng giác.
g'(x) = (sin(x))' + (cos(x))'
g'(x) = cos(x) - sin(x)
Lưu ý quan trọng:
Khi tính đạo hàm, học sinh cần chú ý đến các quy tắc đạo hàm và đạo hàm của các hàm số cơ bản. Ngoài ra, cần thực hiện các phép tính cẩn thận để tránh sai sót.
Bài tập tương tự:
Để luyện tập thêm, học sinh có thể giải các bài tập tương tự trong SGK Toán 11 tập 1 hoặc các đề thi thử Toán 11.
Ứng dụng của đạo hàm:
Đạo hàm có nhiều ứng dụng trong thực tế, như:
Kết luận:
Bài 5.8 trang 141 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các quy tắc tính đạo hàm và phương pháp giải, học sinh có thể tự tin giải quyết các bài tập tương tự và ứng dụng đạo hàm vào các bài toán thực tế.
Bảng tổng hợp các quy tắc đạo hàm cơ bản:
| Hàm số f(x) | Đạo hàm f'(x) |
|---|---|
| c (hằng số) | 0 |
| xn | nxn-1 |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| ex | ex |
| ln(x) | 1/x |