Bài 1.5 trang 7 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng tính giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng các định nghĩa và tính chất của giới hạn để tìm ra kết quả chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 1.5 trang 7, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trên đường tròn lượng giác, tìm điểm biểu diễn của các góc lượng giác có số đo sau:
Đề bài
Trên đường tròn lượng giác, tìm điểm biểu diễn của các góc lượng giác có số đo sau:
a) \( - \frac{{41\pi }}{4}\)
b) \(\frac{{11\pi }}{3}\)
c) 7800
d) -4050
Phương pháp giải - Xem chi tiết
Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\alpha \) là điểm M trên đường tròn lượng giác sao cho sđ(OA, OM) = \(\alpha \).
Lời giải chi tiết
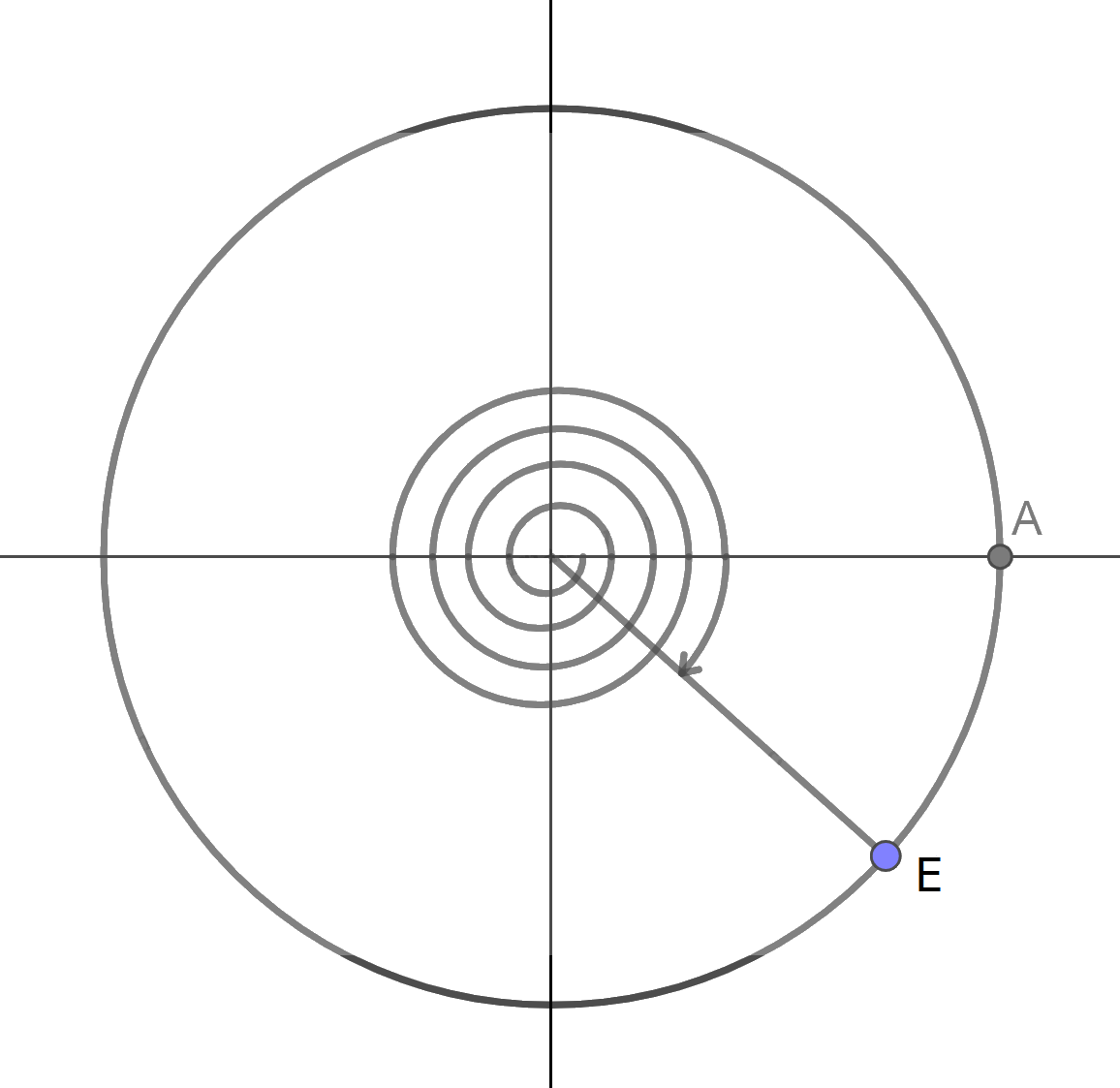
a) Điểm E trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \( - \frac{{41\pi }}{4}\) được xác định như trên hình.
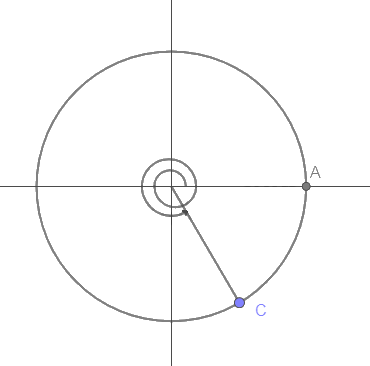
b) Điểm C trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\frac{{11\pi }}{3}\) được xác định như trên hình.
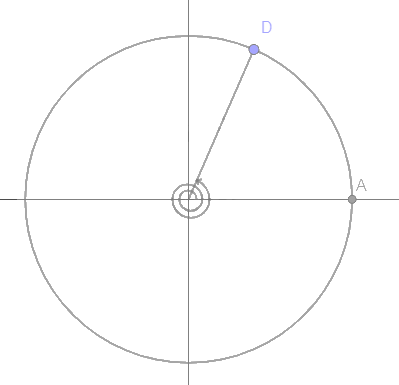
c) Điểm D trên đường tròn lượng giác biểu diễn góc lượng giác có số đo 7800 được xác định như trên hình.
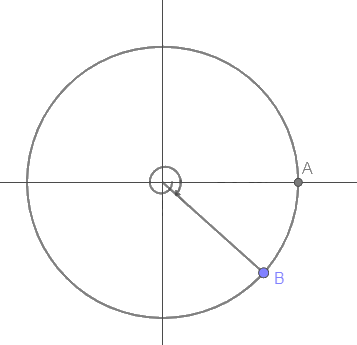
d) Điểm B trên đường tròn lượng giác biểu diễn góc lượng giác có số đo -4050 được xác định như trên hình.
Bài 1.5 trang 7 SGK Toán 11 tập 1 yêu cầu tính các giới hạn sau:
Ta có thể phân tích tử thức:
x² - 3x + 2 = (x - 1)(x - 2)
Vậy:
lim (x→2) (x² - 3x + 2) / (x - 2) = lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1) = 2 - 1 = 1
Ta có thể phân tích tử thức theo công thức hiệu hai lập phương:
x³ - 27 = (x - 3)(x² + 3x + 9)
Vậy:
lim (x→3) (x³ - 27) / (x - 3) = lim (x→3) (x - 3)(x² + 3x + 9) / (x - 3) = lim (x→3) (x² + 3x + 9) = 3² + 3*3 + 9 = 9 + 9 + 9 = 27
Để tính giới hạn này, ta sử dụng phương pháp nhân liên hợp:
lim (x→0) (√(x+1) - 1) / x = lim (x→0) [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)]
= lim (x→0) (x+1 - 1) / [x(√(x+1) + 1)] = lim (x→0) x / [x(√(x+1) + 1)] = lim (x→0) 1 / (√(x+1) + 1)
= 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Giới hạn là một khái niệm cơ bản và quan trọng trong Toán học, được sử dụng rộng rãi trong nhiều lĩnh vực như:
Để củng cố kiến thức về giới hạn, bạn có thể luyện tập thêm các bài tập tương tự trong SGK Toán 11 tập 1 và các tài liệu tham khảo khác.
Bài 1.5 trang 7 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về khái niệm giới hạn và các phương pháp tính giới hạn. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, bạn sẽ tự tin hơn trong việc giải các bài tập tương tự.