Bài 4.1 trang 94 SGK Toán 11 tập 1 thuộc chương trình học Toán 11, tập trung vào việc giải các phương trình lượng giác cơ bản. Bài tập này giúp học sinh rèn luyện kỹ năng biến đổi lượng giác và áp dụng các công thức để tìm nghiệm của phương trình.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.1 trang 94, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
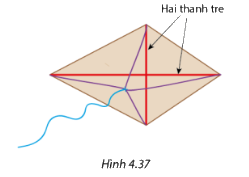
Thả diều là một trong những trò chơi dân gian được nhiều bạn nhỏ yêu thích. Để tự thiết kế một cánh diều từ giấy và thanh tre có nhiều cách khác nhau, nhưng trong trường hợp đơn giản nhất, người ta thường dùng hai thanh tre nẹp vào giấy và buộc nút thắt như Hình 4.37. Hai thanh tre này có tác dụng gì?
Đề bài
Thả diều là một trong những trò chơi dân gian được nhiều bạn nhỏ yêu thích. Để tự thiết kế một cánh diều từ giấy và thanh tre có nhiều cách khác nhau, nhưng trong trường hợp đơn giản nhất, người ta thường dùng hai thanh tre nẹp vào giấy và buộc nút thắt như Hình 4.37. Hai thanh tre này có tác dụng gì?
Phương pháp giải - Xem chi tiết
Quan sát thực tế.
Lời giải chi tiết
Hai thanh tre này cắt nhau giúp cánh diều tạo thành 1 mặt phẳng từ đó giúp diều bay được cao.
Bài 4.1 yêu cầu giải các phương trình lượng giác sau:
Phương trình sin(x) = 1/2 có nghiệm là:
Giải thích:
Ta biết rằng sin(π/6) = 1/2. Do đó, một nghiệm của phương trình là x = π/6. Vì sin(x) = sin(π - x), nên nghiệm còn lại là x = π - π/6 = 5π/6. Tổng quát, ta cộng k2π vào mỗi nghiệm để có tất cả các nghiệm của phương trình.
Phương trình cos(x) = -√3/2 có nghiệm là:
Giải thích:
Ta biết rằng cos(5π/6) = -√3/2. Do đó, một nghiệm của phương trình là x = 5π/6. Vì cos(x) = cos(-x), nên nghiệm còn lại là x = -5π/6 + 2π = 7π/6. Tổng quát, ta cộng k2π vào mỗi nghiệm để có tất cả các nghiệm của phương trình.
Phương trình tan(x) = 1 có nghiệm là:
Giải thích:
Ta biết rằng tan(π/4) = 1. Vì tan(x) có chu kỳ π, nên nghiệm tổng quát là x = π/4 + kπ.
Phương trình cot(x) = 0 có nghiệm là:
Giải thích:
Cot(x) = 1/tan(x). Cot(x) = 0 khi tan(x) tiến tới vô cùng, điều này xảy ra khi x = π/2 + kπ.
Giải phương trình lượng giác có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
Để củng cố kiến thức về giải phương trình lượng giác, các em có thể luyện tập thêm các bài tập sau:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 4.1 trang 94 SGK Toán 11 tập 1 và tự tin giải các bài tập tương tự.