Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 8 và 9 của sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập về nhà.
Tìm một số thích hợp cho mỗi dấu "?" trong bảng sau, biết \(b = {2^\alpha }\):
Tìm một số thích hợp cho mỗi dấu "?" trong bảng sau, biết \(b = {2^\alpha }\):

Phương pháp giải:
Thay \(\alpha \) = -2, -3 vào \(b = {2^\alpha }\) để tìm b tương ứng.
Thay b = 16, \(\sqrt 2 \), \(\frac{1}{4}\) vào \(b = {2^\alpha }\) để tìm \(\alpha \) tương ứng.
Lời giải chi tiết:
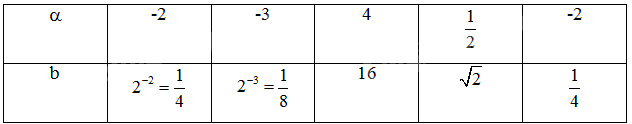
Từ Định nghĩa, với a > 0, \(a \ne 1\) và b > 0, ta có:
\(\alpha = {\log _a}b\,\left( 1 \right) \Leftrightarrow {a^\alpha } = b\left( 2 \right).\)
Tìm một số hoặc biểu thức thích hợp cho mỗi ô ?:
a) Từ (1), khi b = 1 thì \(\alpha \) = ?;
b) Từ (1), khi b = a thì \(\alpha \) = ?;
c) Thay b từ (2) vào (1), ta được ?;
d) Thay \(\alpha \) từ (1) vào (2), ta được ?.
Phương pháp giải:
a) \({\log _a}1 = 0\)
b) \({\log _a}a = 1\)
c) \({\log _a}\left( {{a^\alpha }} \right) = \alpha \)
d) \({a^{{{\log }_a}b}} = b\)
Lời giải chi tiết:
a) \({\log _a}1 = 0 \Rightarrow \alpha = 0\)
b) \({\log _a}a = 1 \Rightarrow \alpha = 1\)
c) \({\log _a}\left( {{a^\alpha }} \right) = \alpha \)
d) \({a^{{{\log }_a}b}} = b\)
Tính \(\log 1000;{\log _{\frac{1}{{\sqrt 3 }}}}9;{\log _2}{4^{\frac{1}{7}}}\) và \({\left( {\frac{1}{{25}}} \right)^{{{\log }_5}\frac{1}{3}}}\).
Phương pháp giải:
Áp dụng: \({\log _a}\left( {{a^\alpha }} \right) = \alpha \) và \({a^{{{\log }_a}b}} = b\)
Lời giải chi tiết:
\(\log 1000 = \log \left( {{{10}^3}} \right) = 3\)
\({\log _{\frac{1}{{\sqrt 3 }}}}9 = {\log _{\frac{1}{{\sqrt 3 }}}}\left( {{{\left( {\frac{1}{{\sqrt 3 }}} \right)}^{ - 4}}} \right) = - 4\)
\({\log _2}{4^{\frac{1}{7}}} = {\log _2}\left( {{2^{\frac{2}{7}}}} \right) = \frac{2}{7}\)
Mục 1 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng trong mục này là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai. Bài viết này sẽ đi sâu vào từng bài tập trong mục 1 trang 8 và 9, cung cấp lời giải chi tiết, dễ hiểu và các lưu ý quan trọng.
Bài 1 thường xoay quanh việc giải các phương trình lượng giác cơ bản như sin(x) = a, cos(x) = a, tan(x) = a, cot(x) = a. Để giải các phương trình này, học sinh cần nắm vững các công thức lượng giác cơ bản, các giá trị đặc biệt của các hàm lượng giác và các bước giải phương trình lượng giác.
Bài 2 thường yêu cầu học sinh giải các phương trình lượng giác phức tạp hơn, đòi hỏi việc sử dụng các công thức biến đổi lượng giác, phương pháp đặt ẩn phụ hoặc phương pháp đưa về phương trình tích.
Ví dụ, để giải phương trình sin(2x) = sin(x), ta có thể sử dụng công thức sin(2x) = 2sin(x)cos(x) để biến đổi phương trình về dạng 2sin(x)cos(x) - sin(x) = 0. Sau đó, ta phân tích thành nhân tử và giải từng phương trình nhỏ.
Bài 3 thường đưa ra các bài toán thực tế liên quan đến phương trình lượng giác, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết. Ví dụ, bài toán về chiều cao của một tòa nhà, góc nhìn từ một điểm nhất định, hoặc chu kỳ của một dao động.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 8 và 9 SGK Toán 11 tập 2:
(Các lời giải chi tiết cho từng bài tập sẽ được trình bày đầy đủ và rõ ràng, kèm theo các bước giải và giải thích cụ thể.)
Hy vọng rằng bài viết này đã giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 8 và 9 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!