Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 2 của chương trình Toán 11 tập 1 thường tập trung vào các kiến thức cơ bản về phép toán, hàm số và các ứng dụng của chúng. Việc giải bài tập một cách chính xác và hiểu rõ bản chất là vô cùng quan trọng.
a) Từ định nghĩa của \(\sin \alpha \)và \(\cos \alpha \), hãy tính \({\sin ^2}\alpha + {\cos ^2}\alpha \). b) Từ định nghĩa của \(\tan \alpha \) và \(\cot \alpha \), hãy tính \(\tan \alpha .\cot \alpha \).
a) Từ định nghĩa của \(\sin \alpha \)và \(\cos \alpha \), hãy tính \({\sin ^2}\alpha + {\cos ^2}\alpha \).
b) Từ định nghĩa của \(\tan \alpha \) và \(\cot \alpha \), hãy tính \(\tan \alpha .\cot \alpha \).
Phương pháp giải:
Lời giải chi tiết:
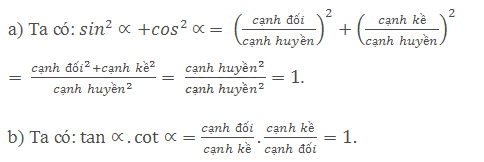
Cường độ ánh sáng I đi xuyên qua một màn lọc ánh sáng được tính bởi công thức \(I = {I_m} - \frac{{{I_m}}}{{1 + {{\cot }^2}\alpha }}\), trong đó Im là cường độ ánh sáng đã chiếu lên màn lọc ánh sáng và là góc \(\alpha \) như trong Hình 1.21 (nguồn: http://www.vedantu.com/iit-jee/malus-law). Chứng minh rằng: \(I = {I_m}{\cos ^2}\alpha \).

Phương pháp giải:
Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
\(\begin{array}{l}I = {I_m} - \frac{{{I_m}}}{{1 + {{\cot }^2}\alpha }} = {I_m}\left( {1 - \frac{1}{{1 + {{\cot }^2}\alpha }}} \right) = {I_m}.\left( {1 - \frac{1}{{\frac{1}{{{{\sin }^2}\alpha }}}}} \right)\\ = {I_m}.\left( {1 - {{\sin }^2}\alpha } \right) = {I_m}.{\cos ^2}\alpha \end{array}\)
a) Dựa vào Hình 1.22, hãy so sánh \(\cos \left( { - \alpha } \right)\) và \(\cos \left( \alpha \right)\); \(\sin \left( { - \alpha } \right)\) và \(\sin \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( { - \alpha } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( { - \alpha } \right)\) và \(\cot \left( \alpha \right)\).

Phương pháp giải:
a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
a) Dựa vào Hình 1.22, ta thấy:
\(\cos \left( { - \alpha } \right)\) = \(\cos \left( \alpha \right)\)
\(\sin \left( { - \alpha } \right) = - \sin \left( \alpha \right)\)
b)
\(\begin{array}{l}\tan \left( { - \alpha } \right) = \frac{{\sin \left( { - \alpha } \right)}}{{\cos \left( { - \alpha } \right)}} = \frac{{ - \sin \alpha }}{{\cos \alpha }} = - \tan \alpha \\\cot \left( { - \alpha } \right) = \frac{{\cos \left( { - \alpha } \right)}}{{\sin \left( { - \alpha } \right)}} = \frac{{\cos \alpha }}{{ - \sin \alpha }} = - \cot \alpha \end{array}\)
a) Dựa vào Hình 1.23, hãy so sánh \(\sin \left( {\pi - \alpha } \right)\) và \(\sin \left( \alpha \right)\); \(\cos \left( {\pi - \alpha } \right)\) và \(\cos \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\pi - \alpha } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( {\pi - \alpha } \right)\) và \(\cot \left( \alpha \right)\).

Phương pháp giải:
a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
a) Dựa vào Hình 1.23, ta thấy:
\(\sin \left( {\pi - \alpha } \right)\) = \(\sin \left( \alpha \right)\)
\(\cos \left( {\pi - \alpha } \right) = - \cos \left( \alpha \right)\)
b) \(\tan \left( {\pi - \alpha } \right) = \frac{{\sin \left( {\pi - \alpha } \right)}}{{\cos \left( {\pi - \alpha } \right)}} = \frac{{\sin \alpha }}{{ - \cos \alpha }} = - \tan \alpha \)
\(\cot \left( {\pi - \alpha } \right) = \frac{1}{{\tan \left( {\pi - \alpha } \right)}} = \frac{1}{{ - \tan \alpha }} = - \cot \alpha \)
a) Dựa vào Hình 1.24, hãy so sánh \(\sin \left( {\alpha + \pi } \right)\) và \(\sin \left( \alpha \right)\); \({\rm{cos}}\left( {\alpha + \pi } \right)\) và \(\cos \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\alpha + \pi } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( {\alpha + \pi } \right)\) và \(\cot \left( \alpha \right)\).

Phương pháp giải:
a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
a) Dựa vào Hình 1.24, ta thấy:
\(\sin \left( {\alpha + \pi } \right) = - \sin \alpha \)
\({\rm{cos}}\left( {\alpha + \pi } \right) = - \cos \alpha \)
b) \(\tan \left( {\alpha + \pi } \right) = \frac{{\sin \left( {\alpha + \pi } \right)}}{{\cos \left( {\alpha + \pi } \right)}} = \frac{{ - \sin \alpha }}{{ - \cos \alpha }} = \tan \alpha \)
\(\cot \left( {\alpha + \pi } \right) = \frac{{\cos \left( {\alpha + \pi } \right)}}{{\sin \left( {\alpha + \pi } \right)}} = \frac{{ - \cos \alpha }}{{ - \sin \alpha }} = \cot \alpha \)
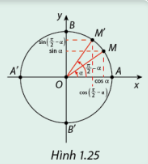
a) Dựa vào Hình 1.25, hãy so sánh \(\sin \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\cos \left( \alpha \right)\); \({\rm{cos}}\left( {\frac{\pi }{2} - \alpha } \right)\) và \(\sin \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\cot \left( \alpha \right)\); \(\cot \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\tan \left( \alpha \right)\).

Phương pháp giải:
a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
a) Dựa vào Hình 1.25, ta thấy:
\(\sin \left( {\frac{\pi }{2} - \alpha } \right)\) = \(\cos \left( \alpha \right)\)
\({\rm{cos}}\left( {\frac{\pi }{2} - \alpha } \right)\) = \(\sin \left( \alpha \right)\)
b) \(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \cot \alpha \)
\(\cot \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}}{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \tan \alpha \)
Chứng minh giá trị của biểu thức sau không phụ thuộc \(\alpha \):
\(B = {\sin ^2}\left( {\alpha + \pi } \right) + {\sin ^2}\left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( { - \alpha } \right) + \cos \left( {\pi - \alpha } \right)\)
Phương pháp giải:
Áp dụng các hệ thức giữa giá trị lượng giác của các góc lượng giác có liên quan đặc biệt.
Lời giải chi tiết:
\(\begin{array}{l}B = {\sin ^2}\left( {\alpha + \pi } \right) + {\sin ^2}\left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( { - \alpha } \right) + \cos \left( {\pi - \alpha } \right)\\ \Leftrightarrow B = {\left( { - \sin \alpha } \right)^2} + {\cos ^2}\alpha + \cos \alpha - \cos \alpha \\ \Leftrightarrow B = {\sin ^2}\alpha + {\cos ^2}\alpha \\ \Leftrightarrow B = 1\end{array}\)
Vậy B không phụ thuộc \(\alpha \).
Mục 2 trong SGK Toán 11 tập 1 thường bao gồm các bài tập về giới hạn của hàm số, đặc biệt là giới hạn tại vô cùng và giới hạn tại một điểm. Việc nắm vững khái niệm giới hạn là nền tảng quan trọng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán học.
Bài tập 1 trang 11 yêu cầu tính giới hạn của hàm số f(x) = 2x + 1 khi x tiến tới 2. Lời giải: lim (x->2) (2x + 1) = 2*2 + 1 = 5.
Bài tập 2 trang 11 yêu cầu tính giới hạn của hàm số g(x) = x^2 - 4 khi x tiến tới 2. Lời giải: lim (x->2) (x^2 - 4) = 2^2 - 4 = 0.
Bài tập 1 trang 12 yêu cầu tính giới hạn của hàm số h(x) = (x - 1) / (x + 1) khi x tiến tới 0. Lời giải: lim (x->0) (x - 1) / (x + 1) = (0 - 1) / (0 + 1) = -1.
Bài tập 2 trang 12 yêu cầu tính giới hạn của hàm số k(x) = sqrt(x) khi x tiến tới 4. Lời giải: lim (x->4) sqrt(x) = sqrt(4) = 2.
Các bài tập từ trang 13 đến trang 15 thường phức tạp hơn, đòi hỏi học sinh phải áp dụng các kỹ năng biến đổi đại số và sử dụng các định lý về giới hạn. Ví dụ, bài tập 1 trang 13 có thể yêu cầu tính giới hạn của một hàm số phân thức phức tạp bằng cách phân tích tử và mẫu thành nhân tử và rút gọn.
Để giải các bài tập này, học sinh cần:
Khi giải bài tập về giới hạn, học sinh cần lưu ý một số điểm sau:
Hy vọng rằng với những hướng dẫn chi tiết và lời giải cụ thể trên đây, các em học sinh đã có thể tự tin giải các bài tập trong Mục 2 trang 11, 12, 13, 14, 15 SGK Toán 11 tập 1. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.