Bài 8.10 trang 63 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải nhanh chóng và hiệu quả, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
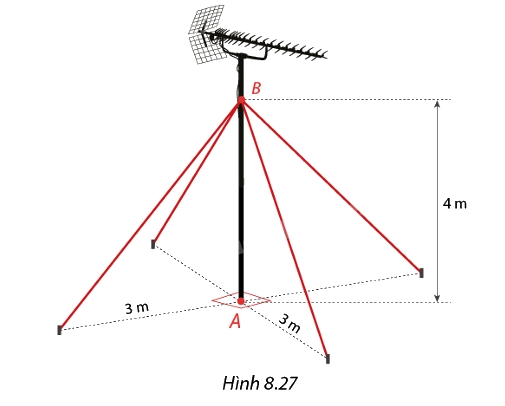
Một cây ăng-ten thẳng đứng với mặt đất và được buộc giằng bởi 4 dây cáp từ một điểm B cách chân A của ăng-ten 4 mét . Khoảng cách từ A đến chân buộc dây giằng bằng 3m ( Hình 8.27).
Đề bài
Một cây ăng-ten thẳng đứng với mặt đất và được buộc giằng bởi 4 dây cáp từ một điểm B cách chân A của ăng-ten 4 mét . Khoảng cách từ A đến chân buộc dây giằng bằng 3m ( Hình 8.27). Tính tổng chiều dài dây cáp để giằng cột ăng- ten ( không tính các mối nối)
Phương pháp giải - Xem chi tiết
Sử dụng định lí Pi – ta – go trong tam giác vuông với hai cạnh góc vuông lần lượt bằng \(3m;\,\,4m\) và dây cáp là cạnh huyền
Từ đó tính được chiều dài một sợi dây cáp và chiều dài của 4 dây cáp
Lời giải chi tiết
Chiều dài 1 dây cáp là \(\sqrt {{4^2} + {3^2}} = 5\)
Chiều dài của 4 dây cáp là \(4.5 = 20m\)
Bài 8.10 trang 63 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc tìm điểm cực trị của hàm số, hoặc xác định khoảng đồng biến, nghịch biến của hàm số. Để giải bài toán này một cách hiệu quả, học sinh cần nắm vững các bước sau:
Giả sử bài toán yêu cầu tìm điểm cực trị của hàm số y = x3 - 3x2 + 2.
Ngoài bài 8.10, SGK Toán 11 tập 2 còn nhiều bài tập tương tự, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán khác nhau. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập về đạo hàm một cách nhanh chóng và hiệu quả, học sinh có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, học sinh có thể tham gia các khóa học online hoặc tìm kiếm sự giúp đỡ từ các gia sư chuyên nghiệp.
Giaitoan.edu.vn cung cấp đầy đủ các bài giải chi tiết, dễ hiểu, cùng với các phương pháp giải nhanh chóng và hiệu quả, giúp học sinh tự tin chinh phục các bài toán về đạo hàm trong chương trình Toán 11.
Việc hiểu rõ bản chất của đạo hàm và ứng dụng của nó trong việc khảo sát hàm số là rất quan trọng. Đạo hàm không chỉ là một công cụ để giải bài tập, mà còn là nền tảng cho các kiến thức toán học nâng cao hơn trong tương lai.
Hãy dành thời gian ôn tập lý thuyết và luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán 11.
Chúc các em học tập tốt!