Bài 5.14 trang 147 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Vũ và Tâm đều theo dõi thành tích của các vận động viên nam trong một cuộc thi bơi tự do dài 50 m. Vũ ghi lại thời gian bơi (đơn vị: giây) của mỗi vận động viên, còn Tâm lập bảng phân bố tần số ghép lớp để biểu diễn kết quả.
Đề bài
Vũ và Tâm đều theo dõi thành tích của các vận động viên nam trong một cuộc thi bơi tự do dài 50 m. Vũ ghi lại thời gian bơi (đơn vị: giây) của mỗi vận động viên, còn Tâm lập bảng phân bố tần số ghép lớp để biểu diễn kết quả.
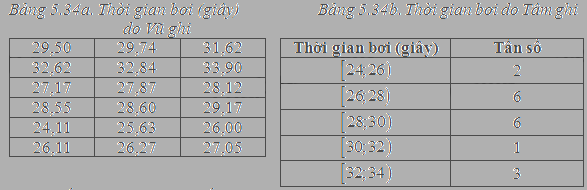
a) Với số liệu do Vũ cung cấp, hãy tính thành tích trung bình của các vận động viên.
b) Với bảng tấn số ghép nhóm của Tâm thì thành tích trung bình của các vận động viên là bao nhiêu?
c) Giải thích vì sao có sự khác nhau giữa hai kết quả tìm được.
Phương pháp giải - Xem chi tiết
a) Số liệu do Vũ ghi theo dạng liệt kê nên trung bình tính theo công thức \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
b) \(\overline x \) của mẫu số liệu ghép nhóm được tính theo công thức
\(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
c) Dựa vào ý nghĩa của công thức tính số trung bình với bảng tần số ghép nhóm
Lời giải chi tiết
a) Thành tích trung bình của các vận động viên là
\(\overline x = \frac{{29,50 + 29,74 + ... + 27,05}}{{18}} = 28,01\) giây
b) Để ngắn gọn, ta trình bày cách tính trung bình của mẫu số liệu ghép nhóm qua bảng sau
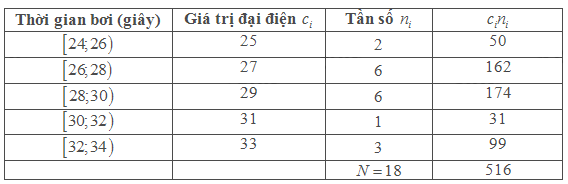
Số trung bình của mẫu số liệu là \(\overline x = \frac{{516}}{{18}} \approx 28,67\) giây
c) Do đối với một mẫu số liệu ghép nhóm, do không biết từng số liệu cụ thể nên ra không tính được giá trị chính xác của số trung bình mà chỉ có thể ước tính gần đúng số trung bình của mẫu.
Bài 5.14 trang 147 SGK Toán 11 tập 1 yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, đặc biệt là các yếu tố như đỉnh, trục đối xứng, và giao điểm với các trục tọa độ để giải quyết một bài toán cụ thể. Bài toán thường liên quan đến việc tìm phương trình đường thẳng đi qua các điểm cho trước hoặc xác định các thông số của parabol.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này bao gồm việc xác định các thông tin đã cho, các đại lượng cần tìm, và các điều kiện ràng buộc. Trong bài 5.14, học sinh cần xác định rõ các điểm, đường thẳng, hoặc các yếu tố khác liên quan đến hàm số bậc hai.
Để giải bài tập hàm số bậc hai, học sinh có thể sử dụng các phương pháp sau:
(Giả sử đề bài: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh, trục đối xứng, và giao điểm với các trục tọa độ.)
Bước 1: Tìm tọa độ đỉnh
a = 1, b = -4, c = 3
Hoành độ đỉnh: x = -b/2a = -(-4)/(2*1) = 2
Tung độ đỉnh: y = (2)2 - 4(2) + 3 = 4 - 8 + 3 = -1
Vậy, tọa độ đỉnh của parabol là (2, -1).
Bước 2: Xác định trục đối xứng
Trục đối xứng là đường thẳng x = 2.
Bước 3: Tìm giao điểm với trục hoành (Ox)
Giải phương trình x2 - 4x + 3 = 0
Δ = (-4)2 - 4(1)(3) = 16 - 12 = 4
x1 = (4 + √4)/(2*1) = (4 + 2)/2 = 3
x2 = (4 - √4)/(2*1) = (4 - 2)/2 = 1
Vậy, giao điểm với trục hoành là (3, 0) và (1, 0).
Bước 4: Tìm giao điểm với trục tung (Oy)
Thay x = 0 vào phương trình hàm số: y = (0)2 - 4(0) + 3 = 3
Vậy, giao điểm với trục tung là (0, 3).
Để nắm vững kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải bài tập, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, học sinh cũng nên tìm hiểu thêm về các ứng dụng của hàm số bậc hai trong thực tế, chẳng hạn như trong vật lý, kỹ thuật, và kinh tế.
Bài 5.14 trang 147 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải bài tập. Bằng cách áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.