Chào mừng bạn đến với bài giải Bài 1.4 trang 7 SGK Toán 11 tập 1 trên giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ bạn học Toán 11 hiệu quả nhất. Hãy cùng khám phá!
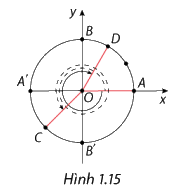
Xác định số đo của các góc lượng giác (OA, OC) và (OA, OD) trong Hình 1.15 (điểm C là điểm chính giữa của cung nhỏ , điểm D là điểm nằm trên cung nhỏ sao cho ). Viết số đo này theo đơn vị radian và theo đơn vị độ.
Đề bài
Xác định số đo của các góc lượng giác (OA, OC) và (OA, OD) trong Hình 1.15 (điểm C là điểm chính giữa của cung nhỏ \(\overset\frown{{{A}^{'}}{{B}^{'}}}\), điểm D là điểm nằm trên cung nhỏ \(\overset\frown{AB}\) sao cho \(\overset\frown{AD}=\frac{2}{3}\overset\frown{AB}\)). Viết số đo này theo đơn vị radian và theo đơn vị độ.
Phương pháp giải - Xem chi tiết
Xác định tia đầu, tia cuối và chiều quay để tìm được số đo của các góc lượng giác.
Lời giải chi tiết
Góc lượng giác có tia đầu là OA, tia cuối là OC, quay theo chiều âm có sđ(OA, OC) = \( {135^0} = \frac{{3\pi }}{4}\).
Góc lượng giác có tia đầu là OA, tia cuối là OD, quay theo chiều dương có sđ(OA, OD) = \(- {60^0} = - \frac{\pi }{3}\).
Bài 1.4 trang 7 SGK Toán 11 tập 1 thuộc chương trình học Toán 11, tập trung vào việc ôn tập về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định các tập hợp, thực hiện các phép hợp, giao, hiệu và phần bù của tập hợp.
Bài tập 1.4 thường bao gồm các câu hỏi yêu cầu:
Để giải quyết hiệu quả các bài tập về tập hợp, bạn cần nắm vững các khái niệm cơ bản sau:
Ví dụ: Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tìm A ∪ B, A ∩ B, A \ B và B \ A.
Giải:
Khi giải bài tập về tập hợp, bạn cần chú ý:
Để củng cố kiến thức về tập hợp, bạn có thể luyện tập thêm với các bài tập tương tự sau:
Kiến thức về tập hợp có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học và các ngành khoa học khác, như:
Bài 1.4 trang 7 SGK Toán 11 tập 1 là một bài tập quan trọng giúp bạn nắm vững kiến thức cơ bản về tập hợp. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, bạn đã hiểu rõ phương pháp giải và có thể tự tin giải quyết các bài tập tương tự. Chúc bạn học tập tốt!