Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 4 trang 112, 113, 114 sách giáo khoa Toán 11 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Cho hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( {\alpha'}\right)\). Trên \(\left( \alpha \right)\), lấy tam giác ABC. Qua các đỉnh A, B, C, ta vẽ các đường thẳng song song với nhau và cắt \(\left( {\alpha '} \right)\) lần lượt tại A, B, C. Các tứ giác ABB′A′, BCC′B′, ACC′A′ là hình gì? Hãy nhận xét về hai tam giác ABC và A′B′C′.
Cho hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( {\alpha'}\right)\). Trên \(\left( \alpha \right)\), lấy tam giác ABC. Qua các đỉnh A, B, C, ta vẽ các đường thẳng song song với nhau và cắt \(\left( {\alpha '} \right)\) lần lượt tại A, B, C. Các tứ giác ABB′A′, BCC′B′, ACC′A′ là hình gì? Hãy nhận xét về hai tam giác ABC và A′B′C′.
Phương pháp giải:
- Cho 2 mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
- Hình bình hành là tứ giác có 2 cặp cạnh đối song song với nhau.
Lời giải chi tiết:
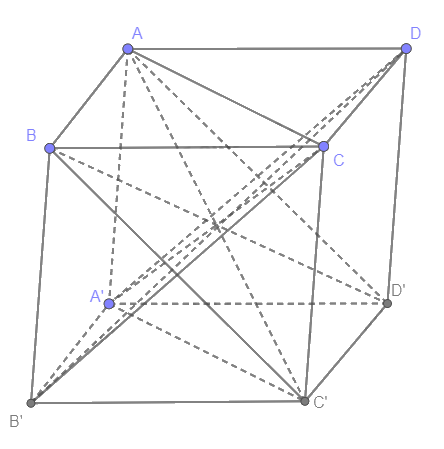
(ABB′A′) cắt 2 mặt phẳng song song \(\left( \alpha \right)\), \(\left( {\alpha '} \right)\) lần lượt theo giao tuyến AB, A’B’. Suy ra AB // A’B’.
Mà AA’ // BB’ nên ABB′A′ là hình bình hành. Do đó AB = A'B'.
(BCC′B′) cắt cắt 2 mặt phẳng song song \(\left( \alpha \right)\), \(\left( {\alpha '} \right)\) lần lượt theo giao tuyến BC, B’C’. Suy ra BC // B’C’.
Mà BB’ // CC’ nên BCC′B′ là hình bình hành. Do đó BC = B'C'.
(ACC′A′) cắt 2 mặt phẳng song song \(\left( \alpha \right)\), \(\left( {\alpha '} \right)\) lần lượt theo giao tuyến AC, A’C’. Suy ra AC // A’C’.
Mà AA’ // CC’ nên ACC′A′ là hình bình hành. Do đó AC = A'C'.
Tam giác ABC và tam giác A'B'C' bằng nhau vì AB = A'B', BC = B'C', AC = A'C'.
Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Gọi O là giao điểm của AC và BD, O' là giao điểm của A'C' và B'D'. Chứng minh rằng AO song song A'O '.
Phương pháp giải:
Cho 2 mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết:

(AA'O'O) cắt 2 mặt phẳng song song (ABCD), (A'B'C'D') theo giao tuyến AO, A'O'. Suy ra AO // A'O'.
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng bốn đường chéo của hình hộp cắt nhau tại trung điểm của mỗi đường.
Phương pháp giải:
Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết:

Ta có ABCD.A'B'C'D' là hình hộp nên AB // C'D' (vì cùng // CD) và AB = C'D' (vì cùng = CD). Suy ra ABC'D' là hình bình hành. Do đó AC' và BD' cắt nhau tại trung điểm của mỗi đường (1)
A'B // CD (vì cùng // AB) và A'B = CD (vì cùng = AB). Suy ra A'BCD là hình bình hành. Do đó A'C và B'D cắt nhau tại trung điểm của mỗi đường (2)
AA' // CC' (vì cùng // BB') và AA' = CC' (vì cùng = BB'). Suy ra ACC'A' là hình bình hành. Do đó AC' và BD' cắt nhau tại trung điểm của mỗi đường (3)
Từ (1), (2), (3) suy ra bốn đường chéo cắt nhau tại trung điểm của mỗi đường.
Mục 4 của SGK Toán 11 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, trước tiên chúng ta cần nắm vững lý thuyết cơ bản liên quan. Hãy bắt đầu bằng việc ôn lại các định nghĩa, định lý và công thức quan trọng.
Nội dung chính của Mục 4:
Hướng dẫn giải chi tiết:
Bài tập 1: (Giải chi tiết bài tập 1 với các bước rõ ràng, sử dụng công thức và giải thích cụ thể). Ví dụ: Để giải bài tập 1, ta thực hiện các bước sau:
Bài tập 2: (Giải chi tiết bài tập 2 với các bước rõ ràng, sử dụng công thức và giải thích cụ thể). Ví dụ: Để giải bài tập 2, ta thực hiện các bước sau:
Bài tập 3: (Giải chi tiết bài tập 3 với các bước rõ ràng, sử dụng công thức và giải thích cụ thể). Ví dụ: Để giải bài tập 3, ta thực hiện các bước sau:
Lưu ý quan trọng:
Mở rộng kiến thức:
Ngoài việc giải các bài tập trong SGK, các em có thể tìm hiểu thêm các bài tập tương tự trong các sách tham khảo hoặc trên internet. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và kỹ năng giải toán.
Tổng kết:
Hy vọng rằng với hướng dẫn chi tiết này, các em đã có thể tự tin giải các bài tập trong mục 4 trang 112, 113, 114 SGK Toán 11 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!