Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 78, 79 SGK Toán 11 tập 2 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho các em học sinh trên con đường chinh phục môn Toán.
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Xét hai đường thẳng chéo nhau AA’ và DC’
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Xét hai đường thẳng chéo nhau AA’ và DC’
a) Đường thẳng A'D' có đồng thời cắt và vuông góc với hai đường thẳng AA’ và D’C không? Vì sao?
b) Tìm mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng AA’ và song song với D’C. So sánh d(D’C, \(\left( \alpha \right)\)) và A’D’.
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
a) Đường thẳng A'D' không đồng thời cắt và vuông góc với hai đường thẳng AA’ và D’C vì A’D’ không vuông góc với D’C.
b) \(\left( \alpha \right)\) là (AA’B)
d(D’C, (AA’B)) = A’D’.
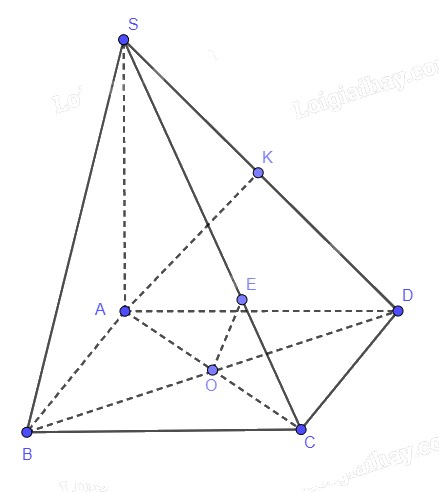
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), SA = 3a; ABCD là hình vuông cạnh a, O là giao điểm của AC và BD. Tính khoảng cách giữa:
a) BD và SC
b) AB và SC.
Phương pháp giải:
a) Tìm khoảng cách giữa a và b:
+ Tìm (P) chứa a và vuông góc với b.
+ Tìm giao điểm H thỏa mãn thuộc b và nằm trong (P).
+ Tại (P), dựng HK vuông góc với a tại K.
+ HK là khoảng cách cần tìm.
b) Tìm khoảng cách giữa a và b:
+ Tìm (P) chứa a và song song với b.
+ \(d\left( {a,b} \right) = d\left( {b,\left( P \right)} \right)\).
Lời giải chi tiết:

a) BD vuông góc với (SAC)
Kẻ OE vuông góc với SC
Vậy OE là khoảng cách cần tìm
\(\begin{array}{l}\frac{1}{{O{E^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{9{a^2}}} + \frac{1}{{2{a^2}}}\\ \Rightarrow OE = \frac{{3\sqrt {22} }}{{11}}a\end{array}\)
b) Kẻ AK vuông góc với SD
Ta có: AB // CD nên AB // (SCD)
\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right) = AK\)
\(\begin{array}{l}AK.SD = SA.AD\\ \Leftrightarrow AK = \frac{{3a.a}}{{\sqrt {{{\left( {3a} \right)}^2} + {a^2}} }} = \frac{{3\sqrt {10} }}{{10}}a\end{array}\)
Mục 3 trong SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể, ví dụ như phép biến hình, hàm số lượng giác, hoặc các ứng dụng của đạo hàm. Việc nắm vững kiến thức lý thuyết và kỹ năng giải bài tập trong mục này là rất quan trọng để chuẩn bị cho các kỳ thi sắp tới.
Để giúp các em hiểu rõ hơn về nội dung bài tập, chúng ta sẽ đi vào giải chi tiết từng bài. Lưu ý rằng, trước khi bắt đầu giải bài tập, các em nên đọc kỹ lý thuyết và ví dụ mẫu trong SGK để nắm vững phương pháp giải.
Đề bài: (Nêu rõ đề bài)
Lời giải:
Giải thích: (Giải thích chi tiết từng bước giải, làm rõ các khái niệm và công thức sử dụng)
Đề bài: (Nêu rõ đề bài)
Lời giải:
Lưu ý: (Nêu các lưu ý quan trọng khi giải bài tập)
Trong mục 3, các em có thể gặp các dạng bài tập sau:
Để giải bài tập Toán 11 tập 2 một cách hiệu quả, các em nên:
Kiến thức trong mục 3 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, chẳng hạn như:
Hy vọng rằng, với bài giải chi tiết và những lời khuyên hữu ích trên đây, các em sẽ tự tin hơn trong việc giải bài tập mục 3 trang 78, 79 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao!
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
| tan x = sin x / cos x | Công thức tính tan x |