Chào mừng bạn đến với bài học về Lý thuyết Công thức nhân xác suất trong chương trình SGK Toán 11 tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về công thức nhân xác suất, giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các dạng bài tập thường gặp và phương pháp giải quyết chúng. Hãy sẵn sàng để khám phá thế giới xác suất đầy thú vị!
A. Lý thuyết 1. Biến cố độc lập
A. Lý thuyết
1. Biến cố độc lập
| Hai biến cố được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia. |
Nhận xét: Nếu A và B là hai biến cố độc lập thì:
- A và \(\overline B \) là hai biến cố độc lập.
- \(\overline A \) và B là hai biến cố độc lập.
- \(\overline A \) và \(\overline B \) là hai biến cố độc lập.
2. Công thức nhân xác suất của hai biến cố độc lập
Nếu A và B là hai biến cố độc lập thì P(AB) = P(A).P(B). |
Lưu ý: Nếu \(P(AB) \ne P(A).P(B)\) thì A và B không độc lập.
3. Sử dụng công thức tổ hợp và sơ đồ hình cây tính xác suất
B. Bài tập
Bài 1: Gieo đồng thời hai con xúc xắc cần đối đồng chất, một màu đỏ một màu xanh và quan sát số chấm xuất hiện trên hai con xúc xắc. Gọi A là biến cố "Số chấm trên mặt xuất hiện của xúc xắc màu đỏ là chẵn" và B là biến cố "Số chấm trên mặt xuất hiện của xúc xắc màu xanh là lẻ". Chỉ ra một cặp biến cố độc lập của phép thử trong và tính xác suất của các biến cố đó.
Giải:
Xét cặp biến cố sau:
A: "Xúc xác màu đỏ xuất hiện mặt 6 chấm".
B: "Xúc xác màu xanh xuất hiện mặt một chấm".
Số phần tử của không gian mẫu, biến cố A và biến cố B lần lượt là:
n(Ω) = 6.6 = 36; n(A) = 6; n(B) = 6.
Do số chấm xuất hiện trên con xúc xác màu đỏ không phụ thuộc vào số chấm xuất hiện trên con xúc xác màu xanh và ngược lại nên việc xảy ra hay không xảy ra biến cố A không làm ảnh hưởng đến xác suất của biến cố B và ngược lại. Do đó biến cố A và B là độc lập. Xác suất của biến cố A và B lần lượt là:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}\); \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}\).
Bài 2: Có hai giỏ trái cây chứa hai loại táo xanh và táo đỏ. Giỏ thứ nhất chứa 5 quả táo xanh và 5 quả táo đỏ. Giỏ thứ hai chứa 4 quả táo xanh và 6 quả táo đỏ. Từ mỗi giỏ lấy ngẫu nhiên một quả táo.
Xét các biến cố:
A: "Quả táo lấy ra từ giỏ thứ nhất màu đỏ".
B: "Quả táo lấy ra từ giỏ thứ hai màu đỏ".
a) Tính P(A), P(B) và P(AB).
b) Tính xác suất để trong hai quả táo lấy ra có ít nhất một quả màu xanh.
Giải:
a) Số phần tử không gian mẫu là n(Ω) = 10.10 = 100.
Số phần tử của biến cố A và B lần lượt là n(A) = 5.10 = 50; n(B) = 6.10 = 60.
Xác suất của các biến cố A và B lần lượt là:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{50}}{{100}} = 0,5\); \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{60}}{{100}} = 0,6\).
Do A và B là hai biến cố độc lập nên P(AB) = P(A).P(B) = 0,5.0,6 = 0,3.
b) Gọi C là biến cố "Hai quả táo lấy ra có ít nhất một quả màu xanh". Khi đó, C là biến cố đối của biến cố AB. Xác suất trong hai quả táo lấy ra có ít nhất một quả màu xanh là:
\(P(C) = P(\overline {AB} ) = 1 - P(AB) = 1 - 0,3 = 0,7\).
Bài 3: Có hai hộp chứa các quả cầu. Hộp thứ nhất chứa 4 quả cầu xanh, 4 quả cầu đỏ và 4 quả cầu vàng. Hộp thứ hai chứa 5 quả cầu xanh, 5 quả cầu đỏ và 5 quả cầu vàng. Lấy ngẫu nhiên từ mỗi hộp 3 quả cầu. Tính xác suất để lấy được 6 quả cầu đỏ.
Giải:
Xét các biến cố:
A: "Ba quả cầu trong hộp thứ nhất là màu đỏ";
B: "Ba quả cầu trong hộp thứ hai là màu đỏ".
Số phần tử của không gian mẫu Ω và các biến cố A, B lần lượt là:
\(n(\Omega ) = C_{12}^3.C_{15}^3\); \(n(A) = C_4^3.C_{15}^3\); \(n(B) = C_5^3.C_{12}^3\).
Xác suất của các biến cố A, B lần lượt là P(A) và P(B):
\(P(A) = \frac{{C_4^3.C_{15}^3}}{{C_{12}^3.C_{15}^3}} = \frac{4}{{220}} = \frac{1}{{55}}\); \(P(A) = \frac{{C_5^3.C_{12}^3}}{{C_{12}^3.C_{15}^3}} = \frac{{10}}{{445}} = \frac{2}{{91}}\).
Do A và B là hai biến cố độc lập nên xác suất để lấy được 6 quả cầu đỏ là:
\(P(AB) = P(A).P(B) = \frac{1}{{55}}.\frac{2}{{91}} = \frac{2}{{5005}}\).
Bài 4: Minh và Nam lần lượt thực hiện một cú sút vào khung thành. Xác suất để Minh sút thành công vào khung thành là 0,6 và Nam sút thành công vào khung thành là 0,7. Sơ đồ cây chưa hoàn thiện bên dưới mô tả các khả năng xảy ra và xác suất tương ứng khi hai bạn lần lượt thực hiện cú sút.
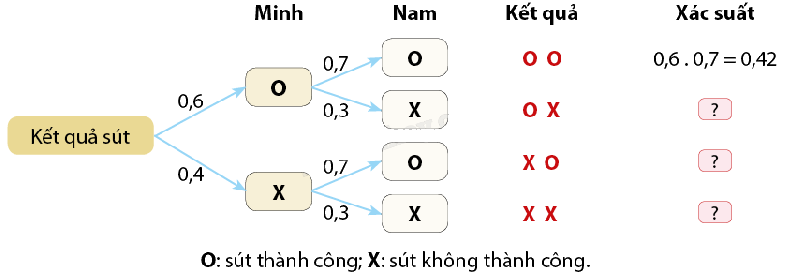
a) Hoàn thiện ba dòng trong cột cuối cùng của sơ đồ hình cây.
b) Tính xác suất để cả hai bạn không sút thành công.
c) Tính xác suất để ít nhất một bạn sút thành công.
Giải:
a) Các phép tính trên ba dòng trong cột cuối cùng của sơ đồ hình cây theo thứ tự là:
0,6.0,3 = 0,18;
0,4.0,7 = 0,28;
0,4.0,3 = 0,12.
b) Xác suất để cả hai bạn không sút thành công là 0,12.
c) Xác suất để có ít nhất một bạn sút thành công là:
0,42 + 0,18 + 0,28 = 0,88.
Công thức nhân xác suất là một trong những công cụ quan trọng nhất trong lý thuyết xác suất, cho phép chúng ta tính xác suất của một sự kiện phức tạp dựa trên xác suất của các sự kiện đơn giản hơn. Bài viết này sẽ trình bày chi tiết về lý thuyết này, bao gồm định nghĩa, các dạng bài tập và phương pháp giải quyết.
Giả sử A và B là hai biến cố độc lập. Xác suất của biến cố A và B đồng thời xảy ra (ký hiệu là P(A∩B)) được tính bằng tích của xác suất của biến cố A và xác suất của biến cố B:
P(A∩B) = P(A) * P(B)
Trong trường hợp A và B không độc lập, công thức nhân xác suất được biểu diễn như sau:
P(A∩B) = P(A) * P(B|A)
Trong đó, P(B|A) là xác suất của biến cố B xảy ra khi biến cố A đã xảy ra (xác suất có điều kiện).
Để giải các bài tập về công thức nhân xác suất, bạn cần thực hiện các bước sau:
Ví dụ 1: Gieo hai con xúc xắc. Tính xác suất để cả hai con xúc xắc đều ra mặt 6.
Giải:
Gọi A là biến cố con xúc xắc thứ nhất ra mặt 6, B là biến cố con xúc xắc thứ hai ra mặt 6. Vì hai biến cố A và B độc lập, ta có:
P(A) = 1/6
P(B) = 1/6
P(A∩B) = P(A) * P(B) = (1/6) * (1/6) = 1/36
Ví dụ 2: Trong một hộp có 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 2 quả bóng. Tính xác suất để cả hai quả bóng đều màu đỏ.
Giải:
Gọi A là biến cố quả bóng thứ nhất lấy được màu đỏ, B là biến cố quả bóng thứ hai lấy được màu đỏ. Hai biến cố A và B không độc lập.
P(A) = 5/8
P(B|A) = 4/7 (vì sau khi lấy một quả bóng đỏ, còn lại 4 quả bóng đỏ và 7 quả bóng tổng cộng)
P(A∩B) = P(A) * P(B|A) = (5/8) * (4/7) = 5/14
Để nắm vững lý thuyết công thức nhân xác suất, bạn nên luyện tập thêm nhiều bài tập khác nhau. Bạn có thể tìm thấy các bài tập này trong SGK Toán 11, các sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Công thức nhân xác suất là một công cụ mạnh mẽ trong lý thuyết xác suất, giúp chúng ta giải quyết các bài toán phức tạp một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết này. Chúc bạn học tập tốt!